题目内容
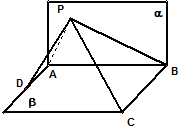 如图,已知平面α⊥平面β,α∩β=AB,C∈β,D∈β,DA⊥AB,CB⊥AB,BC=8,AB=6,AD=4,平面α有一动点P使得∠APD=∠BPC,则△PAB的面积最大值是( )
如图,已知平面α⊥平面β,α∩β=AB,C∈β,D∈β,DA⊥AB,CB⊥AB,BC=8,AB=6,AD=4,平面α有一动点P使得∠APD=∠BPC,则△PAB的面积最大值是( )| A、24 | B、32 | C、12 | D、48 |
考点:平面与平面垂直的性质
专题:空间位置关系与距离
分析:由平面α⊥平面β,α∩β=AB,C∈β,D∈β,DA⊥AB,CB⊥AB,得到△PAD与△PBC是直角三角形,过P点作出AB的垂线PM后,设出AM的长度t,把PM用含有t的代数式表示,求出最大值,代入三角形的面积公式得答案.
解答:
解:由已知平面α⊥平面β,AB是平面α与平面β的交线,
∵C∈β,D∈β,
∴DA?β,CB?β,
又DA⊥AB,CB⊥AB,
∴DA⊥α,CB⊥α,
∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,
∴△PAD∽△PBC,又AD=4,BC=8,∴PB=2PA.
作PM⊥AB,垂足为M,令AM=t∈R,
在两个Rt△PAM与Rt△PBM中,PM是公共边及PB=2PA,
∴PA2-t2=4PA2-(6-t)2 ,解得PA2=12-4t.
∴PM=
,
则(PM)max=4.
∴△PAB的面积最大值S△PAB=
×6×PM=
×6×4=12.
故选:C.
∵C∈β,D∈β,
∴DA?β,CB?β,
又DA⊥AB,CB⊥AB,
∴DA⊥α,CB⊥α,
∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,
∴△PAD∽△PBC,又AD=4,BC=8,∴PB=2PA.
作PM⊥AB,垂足为M,令AM=t∈R,
在两个Rt△PAM与Rt△PBM中,PM是公共边及PB=2PA,
∴PA2-t2=4PA2-(6-t)2 ,解得PA2=12-4t.
∴PM=
| 12-4t-t2 |
则(PM)max=4.
∴△PAB的面积最大值S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查了平面与平面垂直的性质,考查了学生的空间想象能力和思维能力,训练了利用构造方程解题的思想方法,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
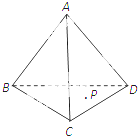 如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )| A、4个 | B、6个 | C、8个 | D、14个 |
在抛物线y2=4x上恒有两点关于直线l:y=kx+3则对称,k的取值范围是( )
| A、-1<k<0 |
| B、0<k<1 |
| C、-1≤k≤0 |
| D、0≤k≤1 |
已知“渐升数”是指每一位数字比其左边的数字大的正整数(如236),那么任取一个三位数,它是渐升数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x、y满足约束条件
,则z=2x+3y的最大值为( )
|
| A、18 | B、2 | C、3 | D、0 |
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
| 3 |
| A、(1,2) | ||
B、(
| ||
C、(1,
| ||
D、(
|
已知0<b<1,0<α<
,x=(sinα)logbsinα,y=(cosα)logbcosα,z=(sinα)logbcosα则三数的大小关系是( )
| π |
| 4 |
| A、x<y<z |
| B、z<x<y |
| C、x<z<y |
| D、y<z<x |



