题目内容
已知函数f（x）=ex-2x-1（其中e为常用对数的底数），则y=f（x）的图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：计算题,函数的性质及应用
分析：找出四个选项的区别，用特值法验证．
解答：
解：∵f（0）=e0-2×0-1=0，f（1）=e-2-1=e-3＜0；
则函数图象过（0，0）点，且在y轴右侧，x轴下方有图象；
故选C．
则函数图象过（0，0）点，且在y轴右侧，x轴下方有图象；
故选C．
点评：本题考查了函数图象的特征，选择题时，首先观察四个选项的区别，利用特值法或基本初等函数的性质排除，从而简化运算步骤．
练习册系列答案
ABC考王全优卷系列答案
相关题目
已知双曲线C：
-
=1（a＞0，b＞0）的左右焦点为F1，F2，且C上一点P满足PF1⊥PF2，|PF1|=3，|PF2|=4，则双曲线C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、5 |
| (1-2sin21)(2cos21-1) |
| A、cos2 | ||
| B、-cos2 | ||
C、cos
| ||
D、-cos
|
函数y=f（x）为定义在R上的减函数，函数y=f（x-1）的图象关于点（1，0）对称，x，y满足不等式f（x2-2x）+f（y2-2y）≥0，则当1≤x≤4时，
的取值范围为（ ）
| y |
| x |
| A、[12，+∞） | ||||
| B、[0，3] | ||||
C、[1-
| ||||
D、（-∞，1-
|
用系统抽样法从已编好号码的500辆车中随机抽出5辆进行试验，则可能选取的车的编号是（ ）
| A、50、100、150、200、250 |
| B、13、113、213、313、413 |
| C、110、120、130、140、150 |
| D、12、40、80、160、320 |
已知函数f（x）=
，若f（x）=ax有且只有一个实数解，则a的取值范围是（ ）
|
| A、[1，2] |
| B、（-∞，0] |
| C、（-∞，0]∪[1，2] |
| D、（-∞，2] |
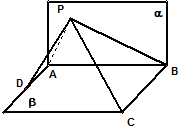如图，已知平面α⊥平面β，α∩β=AB，C∈β，D∈β，DA⊥AB，CB⊥AB，BC=8，AB=6，AD=4，平面α有一动点P使得∠APD=∠BPC，则△PAB的面积最大值是（ ）