题目内容
已知“渐升数”是指每一位数字比其左边的数字大的正整数（如236），那么任取一个三位数，它是渐升数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：求出所有三位数的总数，再求出所有三位“渐升数”的个数，代入古典概型概率计算公式，可得答案．
解答：
解：根据题意，“渐升数”中不能有0，
则在其他9个数字中任取3个，每种取法对应一个“渐升数”，则三位共有“渐升数”C93=84个．
而三位数共有900个，
故任取一个三位数，它是渐升数的概率P=
=
，
故选：B
则在其他9个数字中任取3个，每种取法对应一个“渐升数”，则三位共有“渐升数”C93=84个．
而三位数共有900个，
故任取一个三位数，它是渐升数的概率P=
| 84 |
| 900 |
| 7 |
| 75 |
故选：B
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
| (1-2sin21)(2cos21-1) |
| A、cos2 | ||
| B、-cos2 | ||
C、cos
| ||
D、-cos
|
已知函数y=
在（-∞，-1）上为减函数，则a的范围为（ ）
| 1 |
| x-a |
| A、（-∞，-1） |
| B、（-1，+∞） |
| C、[-1，+∞） |
| D、（-∞，-1] |
已知函数f（x）=3x+x-5的零点x0∈[a，b]，且b-a=1，a，b∈N*，则a+b=（ ）
| A、-2 | B、1 | C、2 | D、3 |
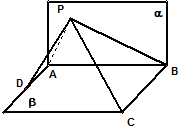如图，已知平面α⊥平面β，α∩β=AB，C∈β，D∈β，DA⊥AB，CB⊥AB，BC=8，AB=6，AD=4，平面α有一动点P使得∠APD=∠BPC，则△PAB的面积最大值是（ ）| A、24 | B、32 | C、12 | D、48 |
已知等比数列{an}的公比为正数，且a3•a9=4a52，a2=6，则a1=（ ）
| A、1 | ||
B、
| ||
| C、3 | ||
| D、2 |
已知函数f（x）=
，若关于x的方程[f（x）]2+bf（x）+2=0有四个不同的正根，则b的取值范围是（ ）
| 1 |
| |x-1| |
A、（-∞，-2
| ||||
B、（-3，-2
| ||||
C、（-3，2
| ||||
D、（-2
|
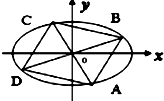已知椭圆C1：