题目内容

9．（1）已知角α的终边上一点P的坐标为$（-\sqrt{3}，2）$，求sinα，cosα和tanα．
（2）在[0°，720°]中与-21°16′终边相同的角有哪些？

分析 （1）利用三角函数的定义求sinα，cosα和tanα．
（2）与-21°16′终边相同的角为k•360°-21°16′（k∈Z），即可求出在[0°，720°]中与-21°16′终边相同的角．

解答 解：（1）由题意，x=-$\sqrt{3}$，y=2，r=$\sqrt{7}$，∴$sinα=\frac{{2\sqrt{7}}}{7}，cosα=-\frac{{\sqrt{21}}}{7}，tanα=-\frac{{2\sqrt{3}}}{3}$
（2）与-21°16′终边相同的角为k•360°-21°16′（k∈Z）
∴在[0°，720°]中与-21°16′终边相同的角有338°44′，698°44′．

点评 本题考查三角函数的定义，考查终边相同的角，属于中档题．

练习册系列答案
相关题目
19．圆的半径为6cm，则圆心角为30°的扇形面积为3π．
20．在平面直角坐标系xoy中，已知向量$\overrightarrow{m}$=（-$\frac{\sqrt{3}}{2}$，$\frac{3}{2}$），$\overrightarrow{n}$=（cosx，sinx），0≤x≤π，且f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$．
（1）若$\overrightarrow{m}$⊥$\overrightarrow{n}$，求tanx的值；
（2）若$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$，求x的值；
（3）求f（x）的单调区间和最值．
17．曲线$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}\right.$（α为参数）上的点到曲线ρcosθ-ρsinθ+1=0的最大距离为$\sqrt{2}+1$．
4．已知函数f（x）=x2+2sinθ•x-1，x∈[-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]．
（1）当sinθ=-$\frac{1}{2}$时，求f（x）的最大值和最小值；
（2）若f（x）在x∈[-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]上是单调函数，且θ∈[0，2π），求θ的取值范围．
14．三棱锥的棱长均为4$\sqrt{6}$，顶点在同一球面上，则该球的表面积为（　　）
A．36πB．72πC．144πD．288π
1．下列四个函数中在（0，+∞）上为增函数的是（　　）
A．f（x）=3-xB．f（x）=（x-1）2C．f（x）=$\frac{1}{x}$D．f（x）=x2+2x
18．如图，PA垂直于矩形ABCD所在的平面，则图中与平面PCD垂直的平面是（　　）
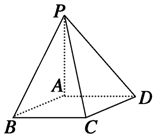
A．平面ABCDB．平面PBCC．平面PADD．平面PBC
19．已知向量$\overrightarrow a=（cosα，2sinα），\overrightarrow b=（2cosβ，-sinβ）$，$α、β∈[0，\frac{π}{2}]$．
（1）若$\overrightarrow a•\overrightarrow b=-\frac{10}{13}$，$sinβ=\frac{4}{5}$，求sin（α+2β）的值；
（2）若$\overrightarrow c=（0，1）$，求$|{\overrightarrow a-\overrightarrow c}|$的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网