题目内容
16．${∫}_{-2}^{2}$（$\sqrt{4-x^2}$+sinx）dx=2π．分析 ${∫}_{-2}^{2}$（$\sqrt{4-x^2}$+sinx）dx=${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx+${∫}_{-2}^{2}$sinxdx，由定积分的几何意义和求解方法可得．
解答 解：${∫}_{-2}^{2}$（$\sqrt{4-x^2}$+sinx）dx=${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx+${∫}_{-2}^{2}$sinxdx，
∵${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx表示圆x2+y2=4与x轴围成的半圆的面积，
∴${∫}_{-2}^{2}$$\sqrt{4-x^2}$dx=$\frac{1}{2}$×π×22=2π，
又${∫}_{-2}^{2}$sinxdx=-cosx${|}_{-2}^{2}$=0，
∴${∫}_{-2}^{2}$（$\sqrt{4-x^2}$+sinx）dx=2π，
故答案为：2π．
点评 本题考查定积分的求解，涉及定积分的几何意义，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．已知a＞b＞m＞0，则（ ）
| A． | $sin\frac{b-m}{a-m}＜sin\frac{b+m}{a+m}＜sin\frac{b}{a}$ | B． | $sin\frac{b-m}{a-m}＞sin\frac{b+m}{a+m}＞sin\frac{b}{a}$ | ||
| C． | $sin\frac{b-m}{a-m}＞sin\frac{b}{a}＞sin\frac{b+m}{a+m}$ | D． | $sin\frac{b-m}{a-m}＜sin\frac{b}{a}＜sin\frac{b+m}{a+m}$ |
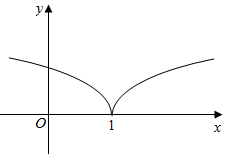如果函数y=f（x）的定义域为R，并且大致图象如图所示，那么函数的解析式可以是f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{ln（2-x），x＜1}\end{array}\right.$（只需写出一个正确答案）