若平面向量$\overrightarrow{a}$=(m.1).$\overrightarrow{b}$=(2.1).且($\overrightarrow{a}$-2$\overrightarrow{b}$)∥$\overrightarrow{b}$.则m=( )A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

13．若平面向量$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（2，1），且（$\overrightarrow{a}$-2$\overrightarrow{b}$）∥$\overrightarrow{b}$，则m=（　　）

A．

B．

C．

D．

分析利用向量的共线的充要条件，列出方程求解即可．

解答解：平面向量$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（2，1），且（$\overrightarrow{a}$-2$\overrightarrow{b}$）∥$\overrightarrow{b}$，
可得m-4=2（-1），
解得m=2．
故选：B．

点评本题考查向量共线的充要条件的应用，考查方程的思想，是基础题．

练习册系列答案

4．

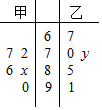一次数学考试后，某老师从自己带的两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学的中位数为73，则x-y的值为（　　）

1．已知复数z满足z+2i、$\frac{z}{2-i}$均为实数，且复数（z+xi）²在复平面上对应的点在第一象限．
（1）求复数z；
（2）求实数x的取值范围．

8．已知向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（1，m），若向量$\overrightarrow{a}$与2$\overrightarrow{a}$-$\overrightarrow{b}$共线，则m=$\frac{1}{3}$．

18．如图，正方形BCDE的边长为a，已知AB=$\sqrt{3}$BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：

①AB与DE所成角的正切值是$\sqrt{2}$；
②AB∥CE
③V_B-ACE体积是$\frac{1}{6}$a³；
④平面ABC⊥平面ADC．
其中正确的有①③④．（填写你认为正确的序号）

5．在△ABC中，角A，B，C的对边分别为a，b，c，已知向量$\overrightarrow{m}$=（cosB，2cos²$\frac{C}{2}$-1），$\overrightarrow{n}$=（c，b-2a），且$\overrightarrow{m}$•$\overrightarrow{n}$=0．
（Ⅰ）求角C的大小；
（Ⅱ）若a+b=6，c=2$\sqrt{3}$，求△ABC的面积．

2．已知向量$\overrightarrow{m}$=（1，2），$\overrightarrow{n}$=（a，-1），若$\overrightarrow{m}$⊥$\overrightarrow{n}$，则实数a的值为（　　）

3．在公差不为0的等差数列{a_n}中，a₂+a₄=a_p+a_q，记$\frac{1}{p}$+$\frac{9}{q}$的最小值为m，若数列{b_n}满足b₁=$\frac{2}{11}$m，2b_n+1-b_n•b_n+1=1，则b₁+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{10{0}^{2}}$=（　　）

试题分类