题目内容
11．设集合M={（x，y）|y=x2+2x}，N={（x，y）|y=x+a}．若M∩N═∅，求a的取值范围．分析 由交集的运算和题意联立抛物线方程和直线方程，消去y后利用△与方程的根的关系，列出不等式求出a的取值范围．
解答 解：联立$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=x+a}\end{array}\right.$得，x2+x-a=0，
则△=12-4×1×（-a）＜0，解得a＜$-\frac{1}{4}$，
所以a的取值范围是（-∞，$-\frac{1}{4}$）．
点评 本题考查交集及其运算，方程组解的个数问题，以及点集的几何意义，考查转化思想．
练习册系列答案
一线名师权威作业本系列答案
相关题目
1．已知i是虚数单位，若复数z满足z=$\frac{{i}^{3}}{1+i}$，则z为（ ）
| A． | $\frac{1+i}{2}$ | B． | $\frac{1-i}{2}$ | C． | $\frac{-1-i}{2}$ | D． | $\frac{-1+i}{2}$ |
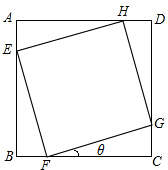如图所示，某住宅小区内有一正方形草地ABCD，现欲在其中修建一个正方形花坛EFGH，若已知花坛面积为正方形草地面积的$\frac{2}{3}$，则θ=arctan（2-$\sqrt{3}$）．
3．下列不等式中成立的是（ ）
| A． | sin140°＜sin30° | B． | cos140°＜cos130° | C． | tan40°＜tan30° | D． | sin40°＜sin30° |