题目内容
5．
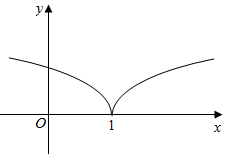如果函数y=f（x）的定义域为R，并且大致图象如图所示，那么函数的解析式可以是f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{ln（2-x），x＜1}\end{array}\right.$（只需写出一个正确答案）
分析 根据函数的对称性以及函数的变化趋势即可写出解析式．
解答 解：如图函数为分段函数，且图象关于x=1对称，故f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{ln（2-x），x＜1}\end{array}\right.$，
故答案为：f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{ln（2-x），x＜1}\end{array}\right.$．
点评 本题考查了函数图象的识别和画法，属于基础题．
练习册系列答案
相关题目
15．设i为虚数单位，则i2014=（ ）
| A． | 1 | B． | i | C． | -1 | D． | -i |
13．在△ABC中，a，b，c分别为内角A、B、C的对边，且满足a=$\sqrt{3}$csinB+bcosC．
（1）求角B的大小；
（2）若a=$\sqrt{3}$，c=4，求△ABC的外接圆的面积．
（1）求角B的大小；
（2）若a=$\sqrt{3}$，c=4，求△ABC的外接圆的面积．
4．
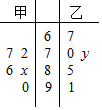一次数学考试后，某老师从自己带的两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学的中位数为73，则x-y的值为（ ）
一次数学考试后，某老师从自己带的两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学的中位数为73，则x-y的值为（ ）| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
2．已知向量$\overrightarrow{m}$=（1，2），$\overrightarrow{n}$=（a，-1），若$\overrightarrow{m}$⊥$\overrightarrow{n}$，则实数a的值为（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |