题目内容
已知f(x)=
是奇函数,且f(2)=
.
(1)求实数p,q的值;
(2)证明函数f(x)在(-∞,-1)上是单调增函数,并判断f(x)在(1,+∞)上的单调性.
| px2+2 |
| 3x+q |
| 5 |
| 3 |
(1)求实数p,q的值;
(2)证明函数f(x)在(-∞,-1)上是单调增函数,并判断f(x)在(1,+∞)上的单调性.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:计算题,证明题,函数的性质及应用
分析:(1)由题意知f(2)=
=
,f(-2)=
=-
;从而解P,q;
(2)化简f(x)=
;求导f′(x)=
(1-
);从而证明函数的单调性,再由奇偶性判断函数的单调性.
| 4p+2 |
| 6+q |
| 5 |
| 3 |
| 4p+2 |
| -6+q |
| 5 |
| 3 |
(2)化简f(x)=
| 2 |
| 3 |
| x2+1 |
| x |
| 2 |
| 3 |
| 1 |
| x2 |
解答:
解:(1)∵f(x)=
是奇函数,
∴f(2)=
=
;
f(-2)=
=-
;
联立解得,p=2,q=0;
(2)证明:f(x)=
;
f′(x)=
(1-
);
∵x∈(-∞,-1),
∴1-
>0,
∴f′(x)>0;
故函数f(x)在(-∞,-1)上是单调增函数;
再由f(x)是奇函数知,
f(x)在(1,+∞)上单调递增.
| px2+2 |
| 3x+q |
∴f(2)=
| 4p+2 |
| 6+q |
| 5 |
| 3 |
f(-2)=
| 4p+2 |
| -6+q |
| 5 |
| 3 |
联立解得,p=2,q=0;
(2)证明:f(x)=
| 2 |
| 3 |
| x2+1 |
| x |
f′(x)=
| 2 |
| 3 |
| 1 |
| x2 |
∵x∈(-∞,-1),
∴1-
| 1 |
| x2 |
∴f′(x)>0;
故函数f(x)在(-∞,-1)上是单调增函数;
再由f(x)是奇函数知,
f(x)在(1,+∞)上单调递增.
点评:本题考查了函数的性质的判断与应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线l:y=-
x+1与x轴所成夹角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知直线l1:2x-y+1=0,l2:x-3y-6=0则l1到l2的角是( )
| A、45° | B、60° |
| C、120° | D、135° |
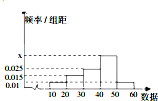 如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.
如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.