题目内容
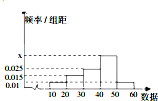 如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.
如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.(Ⅰ)求图中x的值;
(Ⅱ)根据直方图,估计数据的众数和平均数(写出估计值、主要估计依据和方法);
(Ⅲ)已知分布在第一组中有10个数据,求第三组和第四组数据个数之和.
考点:频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据频率和为1,求出x的值;
(Ⅱ)根据直方图中最高矩形的中点,估计出数据的众数,以直方图每个小矩形面积乘以小矩形底边中点的横坐标的积的和,估计平均数;
(Ⅲ)根据频率、频数与样本容量的关系,即可求出结果.
(Ⅱ)根据直方图中最高矩形的中点,估计出数据的众数,以直方图每个小矩形面积乘以小矩形底边中点的横坐标的积的和,估计平均数;
(Ⅲ)根据频率、频数与样本容量的关系,即可求出结果.
解答:
解:(Ⅰ)根据频率和为1,得;
(x+0.01+0.015+0.025+0.01)×10=1,
解得x=0.04;
(Ⅱ)根据直方图中最高矩形的中点,估计数据的众数是
=45;
以直方图每个小矩形面积乘以小矩形底边中点的横坐标的积的和,
估计平均数为:
(15×0.01+25×0.015+35×0.025+45×0.04+55×0.01)×10=37.5;
(Ⅲ)根据直方图知,落在第一组中的数据的频率是0.01×10=0.1,频数是10,
∴该样本的容量是
=100;
又∵第三组和第四组的频率和为(0.025+0.04)×10=0.65,
∴第三组与第四组的数据个数之和为100×0.65=65.
(x+0.01+0.015+0.025+0.01)×10=1,
解得x=0.04;
(Ⅱ)根据直方图中最高矩形的中点,估计数据的众数是
| 40+50 |
| 2 |
以直方图每个小矩形面积乘以小矩形底边中点的横坐标的积的和,
估计平均数为:
(15×0.01+25×0.015+35×0.025+45×0.04+55×0.01)×10=37.5;
(Ⅲ)根据直方图知,落在第一组中的数据的频率是0.01×10=0.1,频数是10,
∴该样本的容量是
| 10 |
| 0.1 |
又∵第三组和第四组的频率和为(0.025+0.04)×10=0.65,
∴第三组与第四组的数据个数之和为100×0.65=65.
点评:本题考查了频率分布直方图的应用问题,也考查了频率=
的应用问题以及众数与平均数的计算问题,是基础题目.
| 频数 |
| 样本容量 |

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
在复平面内,复数
对应的点在( )
| 1 |
| i(i-1) |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,三个内角A、B、C的对边分别为a、b、c,若a=2,b=2
,∠C=15°,则内角A的值为( )
| 2 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,A1B1=A1C1,点D、F分别是棱BC、CC1上的中点,点E是CC1上的动点
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,A1B1=A1C1,点D、F分别是棱BC、CC1上的中点,点E是CC1上的动点