题目内容
在等差数列{an}中，a5+a13=40，则a8+a9+a10=（ ）
| A、72 | B、60 | C、48 | D、36 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：先利用等差中项的性质得出a9=20，再结合a8+a9+a10=3a9即可得出结论．
解答：
解：因为数列{an}是等差数列
所以由a5+a13=40以及等差中项
可得：2a9=40⇒a9=20．
故：a8+a9+a10=3a9=60．
故选：B．
所以由a5+a13=40以及等差中项
可得：2a9=40⇒a9=20．
故：a8+a9+a10=3a9=60．
故选：B．
点评：本题主要考查等差数列中等差中项的性质：即am+an=a
，其中m，n，
都是正整数．
| m+n |
| 2 |
| m+n |
| 2 |
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
掷两枚骰子，出现点数之和为3的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
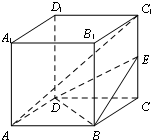如图，在边长为2的正方体ABCD-A1B1C1D1中，E是棱CC1的中点．