题目内容
已知函数f(x)=
.
(1)若m为正常数,求x∈[1,2]上的最小值;
(2)若对?x∈[1,+∞﹚,f﹙x﹚>0恒成立,求实数m的范围.
| x2+2x+m |
| x |
(1)若m为正常数,求x∈[1,2]上的最小值;
(2)若对?x∈[1,+∞﹚,f﹙x﹚>0恒成立,求实数m的范围.
考点:函数恒成立问题
专题:综合题,导数的综合应用
分析:(1)求导数,再结合x∈[1,2],分类讨论,即可求x∈[1,2]上的最小值;
(2)对?x∈[1,+∞﹚,f﹙x﹚>0恒成立等价于?x∈[1,+∞﹚,x2+2x+m>0恒成立,分离参数,求最值,即可求实数m的范围.
(2)对?x∈[1,+∞﹚,f﹙x﹚>0恒成立等价于?x∈[1,+∞﹚,x2+2x+m>0恒成立,分离参数,求最值,即可求实数m的范围.
解答:
解:(1)f(x)=
=x+
+2,则f′(x)=1-
=0,
∴x=
(负值舍去),
∴
>2,即m>4时,f(x)min=f(2)=4+
;
1≤
≤2,即1≤m≤4时,f(x)min=f(
)=2
+2;
<1,即0<m<1时,f(x)min=f(1)=3+m;
(2)对?x∈[1,+∞﹚,f﹙x﹚>0恒成立等价于?x∈[1,+∞﹚,x2+2x+m>0恒成立,
∴m>-(x2+2x).
∵-(x2+2x)=-(x+1)2+1,x∈[1,+∞﹚,
∴x=1时,[-(x2+2x)]max=-3,
∴m>-3.
| x2+2x+m |
| x |
| m |
| x |
| m |
| x2 |
∴x=
| m |
∴
| m |
| m |
| 2 |
1≤
| m |
| m |
| m |
| m |
(2)对?x∈[1,+∞﹚,f﹙x﹚>0恒成立等价于?x∈[1,+∞﹚,x2+2x+m>0恒成立,
∴m>-(x2+2x).
∵-(x2+2x)=-(x+1)2+1,x∈[1,+∞﹚,
∴x=1时,[-(x2+2x)]max=-3,
∴m>-3.
点评:本题考查函数恒成立问题,考查导数知识的运用,考查学生的计算能力,解决本题的关键是对问题进行等价转化,变为函数的最值解决.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知不等式组
表示的平面区域的面积等于3,则a的值为( )
|
| A、-1 | ||
B、
| ||
| C、2 | ||
D、
|
设全集U=R,集合A={x|0<x≤2},B={x|x<1},则集合∁U(A∪B)=( )
| A、(-∞,2] |
| B、(-∞,1] |
| C、(2,+∞) |
| D、[2,+∞) |
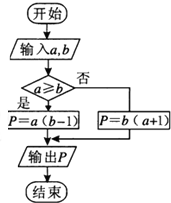 定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输入a=2cos
定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输入a=2cos