Question

已知点P（0，2），设直线l：y=kx+b（k，b∈R）与圆C：x²+y²=4相交于异于点P的A，B两点．
（1）若

PA

•

PB

=0，求b的值；
（2）若|AB|=2

3

，且直线l在两坐标轴上的截距相等，求直线l的方程；
（3）当|PA|•|PB|=4，时，试证明点P到直线l的距离为定值，并求出该定值．

Answer 1

考点：平面向量数量积的运算,点到直线的距离公式

专题：平面向量及应用,直线与圆

分析：（1）根据题意，直线l过圆心O，由此求出b的值；
（2）当|AB|=2

3

时，利用截距相等，设出直线l的方程，
由圆心O到直线l的距离，求出a的值；
（3）当|PA|•|PB|=4时，用特殊点法求出点P到直线l的距离，再证明点P到直线l的距离是定值即可．

解答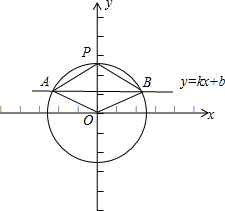： 解：（1）∵点P（0，2）在圆C：x²+y²=4上，且直线l：y=kx+b与圆C交于A，B两点，
当

PA

•

PB

=0时，

PA

⊥

PB

，
∴直线l过圆心O（0，0），∴b=0；
（2）当|AB|=2

3

，且直线l在两坐标轴上的截距相等时，b≠0；
设直线l的方程为x+y=a，
则圆心O（0，0）到直线l：x+y-a=0的距离是
d=

r2-( |AB| 2 )2

，
即

|-a|

2

=

22- (2 3 )2 4

，
解得a=±

2

，
∴直线l的方程为x+y+

2

=0，或x+y-

2

=0；
（3）当|PA|•|PB|=4时，用特殊点法求出点P到直线l的距离为1，如图所示；
现在证明1是点P（0，2）到直线l：y=kx+b=0的距离的定值；
由点P（0，2）到直线l：y=kx+b=0的距离是1，
∴

|-2+b|

1+k2

=1，
∴（b-2）²=1+k²，
∴k²=b²-4b+3；
设A（x₁，y₁），B（x₂，y₂），
由

y=kx+b x2+y2=4

，消去y，
得x²+（kx+b）²=4
（k²+1）x²+2kbx+b²-4=0；
∴x₁+x₂=-

2kb

k2+1

，x₁x₂=

b2-4

k2+1

；
∵|PA|•|PB|=4，∴

x12+(y1-2)2

•

x22+(y2-2)2

=4，
∴（x12+y12-4y₁+4）（x22+y22-4y₂+4）=16，
∴（4-4y₁+4）（4-4y₂+4）=16，
∴（2-y₁）（2-y₂）=1，
∴y₁y₂-2（y₁+y₂）+3=0；
即（kx₁+b）（kx₂+b）-2（kx₁+b+kx₂+b）+3=0，
k²x₁x₂+（kb-2k）（x₁+x₂）-4b+3=0，
∴k²•

b2-4

k2+1

+（kb-2b）•（-

2kb

k2+1

）-4b+3=0，
化简得k²=b²-4b+3；
即证点P到直线l的距离为定值，且定值为1．

点评：本题考查了平面向量的应用问题，也考查了直线与圆的应用问题，考查了定值的应用问题，是综合性题目．