题目内容

将一高和底面直径都等于2的金属圆柱熔成一个金属球（不计损耗），求得到的球的表面积．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：利用等体积，求出球的半径，再求得到的球的表面积．
解答： 解：高和底面直径都等于2的金属圆柱体积为π×12×2=2π，
设球的半径为R，则
4
3
πR3=2π，
∴R=
312
2
，
∴球的表面积S=4πR2=2
318
π．
点评：本题考查球的体积与球的表面积，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知点P（0，2），设直线l：y=kx+b（k，b∈R）与圆C：x2+y2=4相交于异于点P的A，B两点．
（1）若
PA
•
PB
=0，求b的值；
（2）若|AB|=2
3
，且直线l在两坐标轴上的截距相等，求直线l的方程；
（3）当|PA|•|PB|=4，时，试证明点P到直线l的距离为定值，并求出该定值．
函数y=log0.5（-x2+6x-5）在区间（a，a+1）上递减，则实数a的取值范围是
 
．
已知命题p：?x0∈R，sinx0≥
1
2
，则￢p是（　　）
A、?x0∈R，sinx0≤
1
2
B、?x0∈R，sinx0＜
1
2
C、?x∈R，sinx≤
1
2
D、?x∈R，sinx＜
1
2
若a2+b2=1，c2+d2=1，则下面的不等式中正确的是（　　）
A、abcd≤
1
4
B、abcd≥
1
4
C、0≤abcd≤
1
4
D、-
1
4
≤abcd≤
1
4
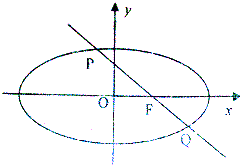已知椭圆的中心在原点，右焦点为F（3，0）过焦点F的直线l交P，Q两点线段PQ的中点为M（2，1）．求：
（1）直线l的方程；
（2）椭圆的标准方程；
（3）线段PQ的长度．
直线2x-y=7与直线3x+2y-7=0的交点坐标是
 
．
已知函数f（x）=
-f(x+3)，x≤2015
x，x＞2015
，则f（1）=
 
．
O为坐标原点，F为抛物线C：y2=4x的焦点，P为C上一点，若∠OFP=120°，S△POF=（　　）
A、
3
B、2
3
C、
3
3
或
3
D、
3
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网