题目内容

化简：（a2-2+a-2）÷（a2-a-2）
考点：有理数指数幂的化简求值
专题：计算题,函数的性质及应用
分析：由题意，原式=
a4-2a2+1
a2
÷
a4-1
a2
=
a4-2a2+1
a4-1
，利用平方公式化简．
解答： 解：原式=
a4-2a2+1
a2
÷
a4-1
a2

=
a4-2a2+1
a4-1

=
(a2-1)2
(a2-1)(a2+1)

=
a2-1
a2+1
．
点评：本题考查了有理指数幂的化简与求值，属于基础题．
练习册系列答案
相关题目
将下列复数的代数形式化为三角形式
（1）z1=2-2i；（2）z2=-1+
3i
；（3）z3=2；（4）z4=2i．
等差数列{an}中，a2=8，S10=185，则数列{an}的通项公式an=
 
（n∈N*）．
在等差数列{an}中，2a4+a7=3，则数列{an}的前9项和等于
 
．
已知点P（0，2），设直线l：y=kx+b（k，b∈R）与圆C：x2+y2=4相交于异于点P的A，B两点．
（1）若
PA
•
PB
=0，求b的值；
（2）若|AB|=2
3
，且直线l在两坐标轴上的截距相等，求直线l的方程；
（3）当|PA|•|PB|=4，时，试证明点P到直线l的距离为定值，并求出该定值．
在△ABC中，内角A、B、C的对边分别a、b、c，若
a
b
=
b+
3
c
a
，sinC=2
3
sinB，则tana=（　　）
A、
3
B、1
C、
3
3
D、-
3
函数f（x）=log0.2（x2-2x+2）的单调递减区间是（　　）
A、[1，+∞）
B、[1，2]
C、[1，2）
D、[2，+∞）
已知ab＞0，下面四个等式中，正确的命题为
 
．
①lg（ab）=lga+lgb；
②lg
a
b
=lga-lgb；
③
1
2
lg（
a
b
）2=lg
a
b
；
④lg（ab）=
1
logab10
．
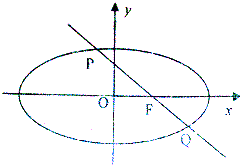已知椭圆的中心在原点，右焦点为F（3，0）过焦点F的直线l交P，Q两点线段PQ的中点为M（2，1）．求：
（1）直线l的方程；
（2）椭圆的标准方程；
（3）线段PQ的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网