题目内容
已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)<0(a,b∈R,a<b),则函数f(x)在(a,b)内( )
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,“f(a)•f(b)<0”根据零点定理f(x)在区间[a,b]上至少有一个零点.
解答:
解:函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,“f(a)•f(b)<0”
∴函数f(x)在区间[a,b]上至少有一个零点,也可能有2,3或多个零点,
故选C.
∴函数f(x)在区间[a,b]上至少有一个零点,也可能有2,3或多个零点,
故选C.
点评:本题考查零点的存在性定理,属于一道基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=2ax+
(a∈R).
(1)当0<a≤
时,试判断f(x)在(0,1]上的单调性并用定义证明你的结论;
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
| 1 |
| x |
(1)当0<a≤
| 1 |
| 2 |
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
下列函数是奇函数的是( )
A、y=x -
| ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x2,x∈[0,1] |
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 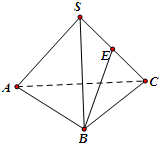
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |
已知正方体ABCD-A1B1C1D1中,平面BDC1∩平面A1B1C1D1=l,则直线BD与交线l的位置关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
若某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是( )cm3


| A、π | B、2π | C、3π | D、4π |
| a |
| b |
| A、a>b | B、a>b>0 |
| C、a<b | D、b<a<0 |