题目内容
在边长为4的正方形ABCD中,AC与BD相交于O.减去△AOB,将剩下部分沿OC、OD折叠,使OA、OB重合,则以A(B),C,D,O为顶点的四面体的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:如图所示,折叠后的四面体.其中AO⊥底面OCD,OC⊥OD.边长为4的正方形ABCD中,AC与BD相交于O.
可得AO=OC=OD=2
.利用三棱锥的体积计算公式即可得出.
可得AO=OC=OD=2
| 2 |
解答:
解:如图所示,折叠后的四面体.
其中AO⊥底面OCD,OC⊥OD.
∵边长为4的正方形ABCD中,AC与BD相交于O.
∴AO=OC=OD=2
.
∴以A(B),C,D,O为顶点的四面体的体积=
•OA•S△COD
=
×2
×
×(2
)2
=
.
故选:A.

其中AO⊥底面OCD,OC⊥OD.
∵边长为4的正方形ABCD中,AC与BD相交于O.
∴AO=OC=OD=2
| 2 |
∴以A(B),C,D,O为顶点的四面体的体积=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
=
8
| ||
| 3 |
故选:A.
点评:本题考查了三棱锥的体积计算公式、图形的折叠问题,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知实数x、y满足
,则目标函数z=x2+y2的最小值为( )
|
A、
| ||
| B、2 | ||
| C、1 | ||
| D、5 |
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 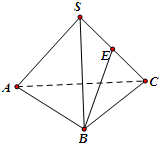
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |
已知正数x、y满足
,则z=(
)x•(
)y的最小值为( )
|
| 1 |
| 4 |
| 1 |
| 2 |
A、
| |||
B、
| |||
C、2
| |||
| D、4 |