题目内容
函数f(x)=xlog2x-3的零点所在区间为(k,k+1)(k∈Z),则k的值是 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:求f′(x),判断函数f(x)取得最值的情况,以及取得零点的情况,及零点的个数,并且能够得到函数f(x)只有一个零点,并且是在(2-ln2,+∞)内.容易判断f(2)<0,f(3)>0,所以零点在区间(2,3)内,所以根据已知f(x)在(k,k+1),k∈Z,内有零点,所以k=2.
解答:
解:f′(x)=ln2+log2x,令f′(x)=0得,x=2-ln2,且0<2-ln2<1;
∴x∈(0,2-ln2)时,f′(x)<0,x∈(2-ln2,+∞)时,f′(x)>0;
∴f(x)在(0,2-ln2)上单调递减,在(2-ln2,+∞)上单调递增;
又x趋向于0时,log2x<0,x>0,∴xlog2x<0,即函数f(x)在(0,2-ln2)内不存在零点;
又∵f(2)=2-3<0,f(3)=3log23-3>0;
∴f(x)在区间(2,3)内存在一个零点,且在(2-ln2,+∞)内只有一个零点;
由已知f(x)零点所在区间为(k,k+1),(k∈Z);
∴k=2.
故答案为:2.
∴x∈(0,2-ln2)时,f′(x)<0,x∈(2-ln2,+∞)时,f′(x)>0;
∴f(x)在(0,2-ln2)上单调递减,在(2-ln2,+∞)上单调递增;
又x趋向于0时,log2x<0,x>0,∴xlog2x<0,即函数f(x)在(0,2-ln2)内不存在零点;
又∵f(2)=2-3<0,f(3)=3log23-3>0;
∴f(x)在区间(2,3)内存在一个零点,且在(2-ln2,+∞)内只有一个零点;
由已知f(x)零点所在区间为(k,k+1),(k∈Z);
∴k=2.
故答案为:2.
点评:考查通过判断函数导数符号判断函数单调性的方法,以及函数零点的概念,以及单调函数取得零点的情况.

练习册系列答案
相关题目
已知集合M={a,b,c},集合N满足N⊆M,则集合N的个数是( )
| A、6 | B、7 | C、8 | D、9 |
已知集合A={x|2x2-3x-2<0},集合B={x|
≥1},则A∩B=( )
| 2x+1 |
| x-1 |
A、(-
| ||
| B、(1,2) | ||
| C、[1,2) | ||
D、(-
|
已知函数f(x)=2ax+
(a∈R).
(1)当0<a≤
时,试判断f(x)在(0,1]上的单调性并用定义证明你的结论;
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
| 1 |
| x |
(1)当0<a≤
| 1 |
| 2 |
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
已知实数x、y满足
,则目标函数z=x2+y2的最小值为( )
|
A、
| ||
| B、2 | ||
| C、1 | ||
| D、5 |
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 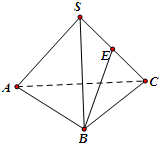
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |
