题目内容
把1+(1+x)+(1+x)2+…+(1+x)n展开成关于x的多项式,其各项系数和为an,则an=( )
| A、2n+1-1 |
| B、2n-1 |
| C、2n+2-1 |
| D、与x有关 |
考点:二项式定理
专题:二项式定理
分析:利用赋值法,通过x=1直接求出展开式各项系数和为an的值.
解答:
解:在1+(1+x)+(1+x)2+…+(1+x)n中,令x=1,可得把它展开成关于x的多项式时,
其各项系数和为an=1+2+22+23+…+2n=
=2n+1-1,
故选:A.
其各项系数和为an=1+2+22+23+…+2n=
| 1×(1-2n+1) |
| 1-2 |
故选:A.
点评:本题考查二项式定理的应用,赋值法以及数列求和的基本方法,考查计算能力,属于基础题.

练习册系列答案
相关题目
已知集合M={a,b,c},集合N满足N⊆M,则集合N的个数是( )
| A、6 | B、7 | C、8 | D、9 |
下列说法正确的是( )
| A、“f(0)=0”是“函数f(x)是奇函数”的充要条件 | ||||||||||||||||||
B、“向量
| ||||||||||||||||||
| C、“?x∈R,x2+1>0”的否定是“?x0∈R,x02+1<0” | ||||||||||||||||||
D、“若a=
|
已知集合A={x|2x2-3x-2<0},集合B={x|
≥1},则A∩B=( )
| 2x+1 |
| x-1 |
A、(-
| ||
| B、(1,2) | ||
| C、[1,2) | ||
D、(-
|
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 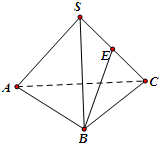
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |