题目内容
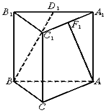 如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是考点:异面直线及其所成的角
专题:空间角
分析:取BC的中点D,连接D1F1,F1D,AD.利用三角形的中位线定理可得D1B∥D1F,因此∠DF1A就是BD1与AF1所成角或其补角.在△DF1A中利用余弦定理即可得出.
解答:
解:取BC的中点D,连接D1F1,F1D,AD.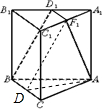
∴D1B∥D1F,∴∠DF1A就是BD1与AF1所成角或其补角.
设BC=CA=CC1=2,则AD=
,AF1=
,DF1=
.
在△DF1A中,利用余弦定理可得cos∠DF1A=
=
.
故答案为:
.

∴D1B∥D1F,∴∠DF1A就是BD1与AF1所成角或其补角.
设BC=CA=CC1=2,则AD=
| 5 |
| 5 |
| 6 |
在△DF1A中,利用余弦定理可得cos∠DF1A=
(
| ||||||
2×
|
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:本题考查了异面直线所成的夹角、三角形的中位线定理、余弦定理、勾股定理等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
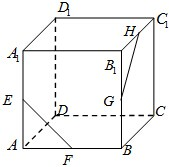 如图,在正方体ABCDA1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCDA1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )| A、30° | B、45° |
| C、60° | D、90° |

