题目内容
设x、y、z∈R+,x2+y2+z2=1,当x+2y+2z取得最大值时,x+y+z= .
考点:柯西不等式在函数极值中的应用
专题:选作题,不等式
分析:考虑到应用柯西不等式(ax+by+cz)2≤(a2+b2+c2)(x2+y2+z2),首先构造出柯西不等式求出(x+2y+2z)2的最大值,开平方根即可得到答案.
解答:
解:根据柯西不等式(ax+by+cz)2≤(a2+b2+c2)(x2+y2+z2)构造得:
即(x+2y+z)2≤(x2+y2+z2)(12+22+22)≤1×9=9
故x+2y+3z≤3.当且仅当x=
=
=
时取等号.
∴x+y+z=
.
故答案为:
,
即(x+2y+z)2≤(x2+y2+z2)(12+22+22)≤1×9=9
故x+2y+3z≤3.当且仅当x=
| y |
| 2 |
| z |
| 2 |
| 1 |
| 3 |
∴x+y+z=
| 5 |
| 3 |
故答案为:
| 5 |
| 3 |
点评:此题主要考查柯西不等式的应用问题,对于此类题目有很多解法,但大多数比较繁琐,而用柯西不等式求解非常简练,需要同学们注意掌握.

练习册系列答案
相关题目
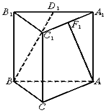 如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是