题目内容
已知函数f(x)=|2x-1|+|x-2a|,若x∈[1,2]时,f(x)≤3恒成立,则实数a= .
考点:带绝对值的函数
专题:转化思想,不等式
分析:由题意,f(x)≤3可化为|x-2a|≤3-|2x-1|,由x∈[1,2],得|x-2a|≤4-2x,即3x-4≤2a≤4-x 对x∈[1,2]恒成立,在x∈[1,2]时,求得3x-4 的最大值和4-x的最小值,即得a的值.
解答:
解:∵f(x)=|2x-1|+|x-2a|,且f(x)≤3,
∴|x-2a|≤3-|2x-1|;
又∵x∈[1,2],
∴|x-2a|≤4-2x,
即 2x-4≤2a-x≤4-2x,
∴3x-4≤2a≤4-x对x∈[1,2]恒成立,
当1≤x≤2时,3x-4的最大值2,4-x的最小值为2,
∴a=1.
故答案为:1.
∴|x-2a|≤3-|2x-1|;
又∵x∈[1,2],
∴|x-2a|≤4-2x,
即 2x-4≤2a-x≤4-2x,
∴3x-4≤2a≤4-x对x∈[1,2]恒成立,
当1≤x≤2时,3x-4的最大值2,4-x的最小值为2,
∴a=1.
故答案为:1.
点评:本题考查了含有绝对值不等式的解法问题,解题时应利用等价转化、分类讨论的数学思想,是中档题.

练习册系列答案
相关题目
经过圆x2+(y+1)2=1的圆心C,且与直线2x+3y-4=0平行的直线方程为( )
| A、2x+3y+3=0 |
| B、2x+3y-3=0 |
| C、2x+3y+2=0 |
| D、3x-2y-2=0 |
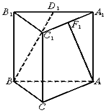 如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是