题目内容
将函数y=
的图象绕x轴旋转一周所形成的几何体的体积为 .
| 4-x2 |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据题意,函数y=
的图象是以原点为圆心、半径等于2的圆的上半部分,即如图所示的半圆.因此题中的旋转体是以O为球心、半径等于2的球,结合球的表面积公式即可得到该旋转体的体积.
| 4-x2 |
解答:
解:将函数y=
平方整理,得x2+y2=4(y≥0)
因此,函数y=
的图象是以原点为圆心、半径等于2的圆的上半部分,
即如图所示的半圆,

∴函数y=
的图象绕x轴旋转一周,
所形成的几何体是以O为球心、半径等于2的球,
结合球的体积公式,
得该旋转体体积为V=
πR3=
,
故答案为:
| 4-x2 |
因此,函数y=
| 4-x2 |
即如图所示的半圆,

∴函数y=
| 4-x2 |
所形成的几何体是以O为球心、半径等于2的球,
结合球的体积公式,
得该旋转体体积为V=
| 4 |
| 3 |
| 32π |
| 3 |
故答案为:
| 32π |
| 3 |
点评:本题给出图象为半圆的函数,求函数图象绕x轴旋转一周形成旋转体的表面积,着重考查了圆的标准方程、函数表达式的化简和球的表面积公式等知识,属于中档题.

练习册系列答案
相关题目
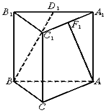 如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是