题目内容
已知关于x的函数y=x2-4ax+2a+6,若y≥0恒成立,则函数f(a)=2-a|a+3|的值域为( )
A、[-
| ||||
B、[-2,
| ||||
C、[-
| ||||
| D、[-2,4] |
考点:二次函数的性质
专题:函数的性质及应用
分析:先根据关于x的函数y=x2-4ax+2a+6,y≥0恒成立可求出a的取值范围:-1≤a≤
,这时候可求出f(a),并判断f(a)在[-1,
]上的单调性,根据单调性即可求出函数f(a)的值域.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:对于函数y=x2-4ax+2a+6,y≥0恒成立,∴△=16a2-4(2a+6)≤0,解得:
-1≤a≤
;
∴f(a)=2-a|a+3|=2-a(a+3)=-(a+
)2+
;
∴f(a)在[-1,
]上单调递减,
∴f(a)∈[f(
),f(-1)]=[-
,4];
即f(a)的值域为[-
,4].
故选C.
-1≤a≤
| 3 |
| 2 |
∴f(a)=2-a|a+3|=2-a(a+3)=-(a+
| 3 |
| 2 |
| 17 |
| 4 |
∴f(a)在[-1,
| 3 |
| 2 |
∴f(a)∈[f(
| 3 |
| 2 |
| 19 |
| 4 |
即f(a)的值域为[-
| 19 |
| 4 |
故选C.
点评:考查二次函数图象和x轴交点情况和判别式△的关系,二次函数的单调性和对称轴的关系.

练习册系列答案
相关题目
已知两点A(cosα,sinα)和B(cos2α,sin2α),则AB的长为( )
A、2sin
| ||
B、2|sin
| ||
C、2cos
| ||
D、2|cos
|
下列各图中,不可能表示函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
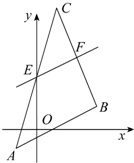 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的