题目内容
下列函数中，与函数y=|x|表示的不是同一个函数的是（ ）
A、y=
| |||||
B、y=
| |||||
C、y=
| |||||
| D、y=2log2|x| |
考点：判断两个函数是否为同一函数
专题：计算题,函数的性质及应用
分析：判断函数是否相等要看两个方面，对应关系与定义域．
解答：
解：A、B、C与函数y=|x|表示的是同一个函数，
D不是，y=2log2|x|的定义域为{x|x≠0}，
而函数y=|x|的定义域为R．
故选D．
D不是，y=2log2|x|的定义域为{x|x≠0}，
而函数y=|x|的定义域为R．
故选D．
点评：本题考查了函数相等的判断，只需对定义域与对应关系两者都判断即可．
练习册系列答案
相关题目
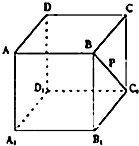如图，点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列结论：①三棱锥A-D1PC的体积不变；②A1P∥平面ACD1；③DP⊥BC1；④平面PDB1⊥平面ACD1．其中正确的结论的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
若在[2，4]上f（x）=loga（ax2-x）是增函数，则a取值范围是（ ）
| A、a＞1 | ||
B、
| ||
C、
| ||
D、0＜a＜
|