题目内容
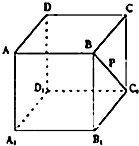如图，点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列结论：①三棱锥A-D1PC的体积不变；②A1P∥平面ACD1；③DP⊥BC1；④平面PDB1⊥平面ACD1．其中正确的结论的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：命题的真假判断与应用
专题：空间位置关系与距离
分析：利用空间中线线、线面、面面间的位置关系，结合线线、线面、面面平行和垂直的判断与性质求解．
解答：
解：
对于①，由题意知AD1∥BC1，从而BC1∥平面AD1C，
故BC1上任意一点到平面AD1C的距离均相等，
所以以P为顶点，平面AD1C为底面，则三棱锥A-D1PC的体积不变，故①正确；
对于②，连接A1B，A1C1，A1C1∥AD1且相等，由于①知：AD1∥BC1，
所以BA1C1∥面ACD1，从而由线面平行的定义可得，故②正确；
对于③，由于DC⊥平面BCB1C1，所以DC⊥BC1，
若DP⊥BC1，则BC1⊥平面DCP，
BC1⊥PC，则P为中点，与P为动点矛盾，故③错误；
对于④，连接DB1，由DB1⊥AC且DB1⊥AD1，
可得DB1⊥面ACD1，从而由面面垂直的判定知，故④正确．
故选：C．
对于①，由题意知AD1∥BC1，从而BC1∥平面AD1C，故BC1上任意一点到平面AD1C的距离均相等，
所以以P为顶点，平面AD1C为底面，则三棱锥A-D1PC的体积不变，故①正确；
对于②，连接A1B，A1C1，A1C1∥AD1且相等，由于①知：AD1∥BC1，
所以BA1C1∥面ACD1，从而由线面平行的定义可得，故②正确；
对于③，由于DC⊥平面BCB1C1，所以DC⊥BC1，
若DP⊥BC1，则BC1⊥平面DCP，
BC1⊥PC，则P为中点，与P为动点矛盾，故③错误；
对于④，连接DB1，由DB1⊥AC且DB1⊥AD1，
可得DB1⊥面ACD1，从而由面面垂直的判定知，故④正确．
故选：C．
点评：本题考查命题真假的判断，解题时要注意三棱锥体积求法中的等积法、线面平行、线线垂直的判定，要注意转化的思想的使用，是中档题．
练习册系列答案
相关题目
已知4tan
=1-tan2
，则tanα的值为（ ）
| α |
| 2 |
| α |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
函数y=x2+2x的减区间是（ ）
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、（-∞，0] |
| D、（-∞，+∞） |
sin10°cos70°-cos10°sin70°=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知正项等比数列{an}中 a2•a6=4，则log2a1+log2a2+…+log2a7=（ ）
| A、5 | B、6 | C、7 | D、8 |
下列函数中，与函数y=|x|表示的不是同一个函数的是（ ）
A、y=
| |||||
B、y=
| |||||
C、y=
| |||||
| D、y=2log2|x| |