题目内容
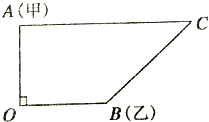 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=| 13 |
考点:向量的加法及其几何意义
专题:直线与圆
分析:以O为原点,OB为x轴,建立直角坐标系,利用|AC|=5km,|BC|=
km,|AO|=|BO|=2km,得到关于x,y的方程组,求出C 的坐标,从而得到AC,边长的方向.
| 13 |
解答:
解:以O为原点,OB为x轴,建立直角坐标系,如图,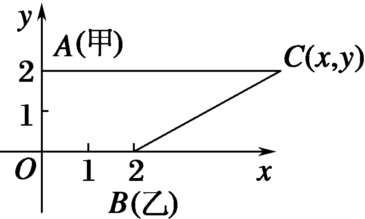
设 C(x,y),则有 A(0,2),B(2,0),由|AC|=5,有 x2+(y-2)2=25,①
|BC|=
,有 (x-2)2+y2=13.②,
由①②解得
或者
,
由x、y的实际意义知 x>0,y>0,∴C(5,2). 而 A(0,2),∴AC∥x 轴,即 AC∥OB.由 B(2,0)、C(5,2),知 kBC=
,
故甲应以与OB平行的方向行走,乙应沿斜率为
的直线向上方行走,才能使他们的行程和最小.

设 C(x,y),则有 A(0,2),B(2,0),由|AC|=5,有 x2+(y-2)2=25,①
|BC|=
| 13 |
由①②解得
|
|
由x、y的实际意义知 x>0,y>0,∴C(5,2). 而 A(0,2),∴AC∥x 轴,即 AC∥OB.由 B(2,0)、C(5,2),知 kBC=
| 2 |
| 3 |
故甲应以与OB平行的方向行走,乙应沿斜率为
| 2 |
| 3 |
点评:本题考查了直线方程的求法;关键是由题意建立坐标系,得到C的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
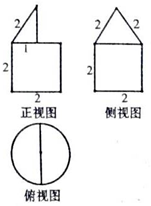
某几何体的三视图如图所示,则该几何体的体积是( )

A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|