题目内容
已知函数f(x)=ax3+bx2(x∈R)的图象过点P(-1,2),且在点P处的斜线斜率为-3,
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
考点:利用导数研究曲线上某点切线方程,有理数指数幂的化简求值,利用导数研究函数的单调性
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)求出f(x)的导数,由条件可得切线的斜率,代入P点,得到a,b的方程,解得即可;
(2)求得f(x)的导数,令导数的大于0,解二次不等式即可得到增区间.
(2)求得f(x)的导数,令导数的大于0,解二次不等式即可得到增区间.
解答:
解:(1)函数f(x)=ax3+bx2的导数为f′(x)=3ax2+2bx,
由在点P处的斜线斜率为-3,即有3a-2b=-3,
f(x)的图象过点P(-1,2),即有-a+b=2,
解得a=1,b=3,
则f(x)=x3+3x2;
(2)函数f(x)=x3+3x2的导数为f′(x)=3x2+6x,
令f′(x)>0,可得x>0或x<-2.
即有f(x)的单调递增区间为(0,+∞),(-∞,-2).
由在点P处的斜线斜率为-3,即有3a-2b=-3,
f(x)的图象过点P(-1,2),即有-a+b=2,
解得a=1,b=3,
则f(x)=x3+3x2;
(2)函数f(x)=x3+3x2的导数为f′(x)=3x2+6x,
令f′(x)>0,可得x>0或x<-2.
即有f(x)的单调递增区间为(0,+∞),(-∞,-2).
点评:本题考查导数的运用:求切线方程和求单调区间,运用导数的几何意义:函数在某点处的导数即为曲线在该点处切线的斜率和二次不等式的解法是解题的关键.

练习册系列答案
相关题目
如图,一个几何体的三视图如图所示,则该多面体的几条棱中,最长的棱的长度为( )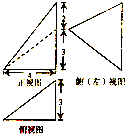

A、3
| ||
B、
| ||
C、
| ||
D、3
|
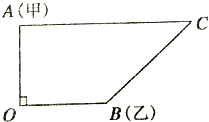 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=