题目内容
已知tan2x=
,求sinx的值.
| 1 |
| 2 |
考点:二倍角的正切,同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件利用二倍角的正切公式求得tanx的值,再利用同角三角函数的基本关系求得sinx的值.
解答:
解:∵tan2x=
=
,∴tanx=-2±
,
当tanx=-2+
时,sec2x=1+tan2x=10-4
,cos2x=
=
,sinx=±
=±
.
当tanx=-2-
时,sec2x=1+tan2x=10+4
,cos2x=
=
,sinx=±
=±
.
综上可得,sinx=±
或sinx=±
.
| 1 |
| 2 |
| 2tanx |
| 1-tan2x |
| 5 |
当tanx=-2+
| 5 |
| 5 |
| 1 |
| sec2x |
5+2
| ||
| 10 |
| 1-cos2x |
| ||||
| 10 |
当tanx=-2-
| 5 |
| 5 |
| 1 |
| sec2x |
5-2
| ||
| 10 |
| 1-cos2x |
| ||||
| 10 |
综上可得,sinx=±
| ||||
| 10 |
| ||||
| 10 |
点评:本题主要考查同角三角函数的基本关系,二倍角的正切公式的应用,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
曲线f(x)=
在点(1,f(1))处切线的倾斜角为
,则实数a=( )
| x2+a |
| x+1 |
| 3π |
| 4 |
| A、1 | B、-1 | C、7 | D、-7 |
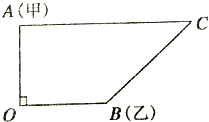 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=