题目内容
关于x的函数f(x)=m(x2-4x+lnx)-(2m2+1)x+2lnx,其中m∈R,函数f(x)在(1,0)处切线斜率为0
(1)求函数f(x)的解析式
(2)已知函数f(x)的图象与直线y=k无公共点,求实数k的取值范围.
(1)求函数f(x)的解析式
(2)已知函数f(x)的图象与直线y=k无公共点,求实数k的取值范围.
考点:利用导数研究曲线上某点切线方程,函数解析式的求解及常用方法
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)求出函数的导数,由函数f(x)在(1,0)处的切线斜率为0,即有f′(1)=0,f(1)=0,列方程可得m=-1,即可得到f(x)的解析式;
(2)求f(x)的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而得到函数的极大值,也为最大值0,再由题意可得k>0.
(2)求f(x)的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而得到函数的极大值,也为最大值0,再由题意可得k>0.
解答:
解:(1)函数f(x)=m(x2-4x+lnx)-(2m2+1)x+2lnx的导数为
f′(x)=m(2x-4+
)-(2m2+1)+
,
函数f(x)在(1,0)处切线斜率为k=-m-2m2+1,
由函数f(x)在(1,0)处切线斜率为0,即有-m-2m2+1=0,
又f(1)=0,即有2m2+3m+1=0,
解得m=-1.
即有f(x)=-x2+x+lnx;
(2)f(x)=-x2+x+lnx的导数为f′(x)=-2x+1+
=
=
,
当x>1时,f′(x)<0,f(x)单调递减,
当0<x<1时,f′(x)>0,f(x)单调递增.
则有f(x)在x=1处取得极大值,也为最大值,且为0,
由于函数f(x)的图象与直线y=k无公共点,
则k>0.
即实数k的取值范围是(0,+∞).
f′(x)=m(2x-4+
| 1 |
| x |
| 2 |
| x |
函数f(x)在(1,0)处切线斜率为k=-m-2m2+1,
由函数f(x)在(1,0)处切线斜率为0,即有-m-2m2+1=0,
又f(1)=0,即有2m2+3m+1=0,
解得m=-1.
即有f(x)=-x2+x+lnx;
(2)f(x)=-x2+x+lnx的导数为f′(x)=-2x+1+
| 1 |
| x |
=
| -2x2+x+1 |
| x |
| -(2x+1)(x-1) |
| x |
当x>1时,f′(x)<0,f(x)单调递减,
当0<x<1时,f′(x)>0,f(x)单调递增.
则有f(x)在x=1处取得极大值,也为最大值,且为0,
由于函数f(x)的图象与直线y=k无公共点,
则k>0.
即实数k的取值范围是(0,+∞).
点评:本题考查导数的运用:求切线的斜率和单调区间及极值、最值,正确求导和求出最大值是解题的关键.

练习册系列答案
相关题目
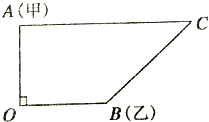 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=