题目内容
已知f(x)是定义在[1,+∞]上的函数,且f(x)=
,则函数y=2xf(x)-3在区间(1,2015)上零点的个数为 .
|
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:令函数y=2xf(x)-3=0,得到方程f(x)=
,从而化函数的零点为方程的根,再转化为两个函数的交点问题,从而解得.
| 3 |
| 2x |
解答:
解:令函数y=2xf(x)-3=0,得到方程f(x)=
,
当x∈[1,2)时,函数f(x)先增后减,在x=
时取得最大值1,
而y=
在x=
时也有y=1;
当x∈[2,22)时,f(x)=
f(
x),在x=3处函数f(x)取得最大值
,
而y=
在x=3时也有y=
;
当x∈[22,23)时,f(x)=
f(
x),在x=6处函数f(x)取得最大值
,
而y=
在x=6时也有y=
;
…,
当x∈[210,211)时,f(x)=
f(
x),在x=1536处函数f(x)取得最大值
,
而y=
在x=1536时也有y=
;
综合以上分析,将区间(1,2015)分成11段,每段恰有一个交点,所以共有11个交点,即有11个零点.
故答案为:11.
| 3 |
| 2x |
当x∈[1,2)时,函数f(x)先增后减,在x=
| 3 |
| 2 |
而y=
| 3 |
| 2x |
| 3 |
| 2 |
当x∈[2,22)时,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而y=
| 3 |
| 2x |
| 1 |
| 2 |
当x∈[22,23)时,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
而y=
| 3 |
| 2x |
| 1 |
| 4 |
…,
当x∈[210,211)时,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 210 |
而y=
| 3 |
| 2x |
| 1 |
| 210 |
综合以上分析,将区间(1,2015)分成11段,每段恰有一个交点,所以共有11个交点,即有11个零点.
故答案为:11.
点评:本题考查了函数的零点与方程的根的关系及函数的交点的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )| A、5π+4 | B、8π+4 |
| C、5π+12 | D、8π+12 |
曲线f(x)=
在点(1,f(1))处切线的倾斜角为
,则实数a=( )
| x2+a |
| x+1 |
| 3π |
| 4 |
| A、1 | B、-1 | C、7 | D、-7 |
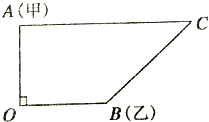 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=