题目内容
解方程组:
.
|
考点:函数的零点与方程根的关系
专题:计算题,推理和证明
分析:由x+y+z=6,可得y+z=6-x,两边平方可得y2+z2+2yz=(6-x)2,可求x,再求出y,z.
解答:
解:由x+y+z=6,可得y+z=6-x,
两边平方可得y2+z2+2yz=(6-x)2,
∴14-x2+4=(6-x)2,
∴x2-6x+9=0,
∴x=3,
∴y+z=3,
∵yz=2,
∴y=1,z=2或y=2,z=1,
∴方程组的解为
或
.
两边平方可得y2+z2+2yz=(6-x)2,
∴14-x2+4=(6-x)2,
∴x2-6x+9=0,
∴x=3,
∴y+z=3,
∵yz=2,
∴y=1,z=2或y=2,z=1,
∴方程组的解为
|
|
点评:本题考查解方程组,考查学生分析解决问题的能力,确定x是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,一个几何体的三视图如图所示,则该多面体的几条棱中,最长的棱的长度为( )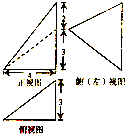

A、3
| ||
B、
| ||
C、
| ||
D、3
|
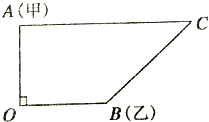 某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=
某二人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5km,|BC|=