题目内容
在数列{an}中,a1=4,an+1=an+k•3n+1(n∈N+,k为常数),a1,a2+6,a3成等差数列.
(1)设数列{bn}满足bn=
,求数列{bn}的前n项和Sn;
(2)设数列{cn}满足cn=
,证明:cn≤
.
(1)设数列{bn}满足bn=
| n |
| an-n |
(2)设数列{cn}满足cn=
| n2 |
| an-n |
| 4 |
| 9 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知得2(a2+6)=a1+a3,解得k=2,从而an+1=an+2•3n+1,由此能求出an=3n+n.从而bn=
=
,由此利用错位相减法能求出数列{bn}的前n项和Sn.
(Ⅱ)由已知得cn=
=
,从而cn+1-cn=
-
=
,由此能证明cn≤
.
| n |
| an-n |
| n |
| 3n |
(Ⅱ)由已知得cn=
| n2 |
| (3n+n)-n |
| n2 |
| 3n |
| (n+1)2 |
| 3n+1 |
| n2 |
| 3n |
| -2n2+2n+1 |
| 3n+1 |
| 4 |
| 9 |
解答:
(Ⅰ)解:因为a1=4,an+1=an+p•3n+1,
所以a2=a1+k•3+1=3k+5,
a3=a2+p•32+1=12k+6.
因为a1,a2+6,a3成等差数列,所以2(a2+6)=a1+a3,
即6k+10+12=4+12k+6,解得k=2.
依题意,an+1=an+2•3n+1,
所以当n≥2时,a2-a1=2•3+1,a3-a2=2•32+1,
…,an-1-an-2=2•3n-2+1,an-an-1=2•3n-1+1.
相加得an-a1=2(3n-1+3n-2+…+32+3)+n-1,
所以an-a1=2×
+(n-1),
所以an=3n+n.
当n=1时,a1=3+1=4成立,
所以an=3n+n.
所以bn=
=
,
所以Sn=
+
+
+…+
,①
Sn=
+
+
+…+
,②
①-②,得:
Sn=
+
+…+
-
=
-
=
-
,
∴Sn=
-
-
.
(Ⅱ)证明:因为an=3n+n,所以cn=
=
.
因为cn+1-cn=
-
=
,(n∈N*).
若-2n2+2n+1<0,则n>
,即n≥2时,cn+1<cn.
又因为c1=
,c2=
,所以cn≤
.
所以a2=a1+k•3+1=3k+5,
a3=a2+p•32+1=12k+6.
因为a1,a2+6,a3成等差数列,所以2(a2+6)=a1+a3,
即6k+10+12=4+12k+6,解得k=2.
依题意,an+1=an+2•3n+1,
所以当n≥2时,a2-a1=2•3+1,a3-a2=2•32+1,
…,an-1-an-2=2•3n-2+1,an-an-1=2•3n-1+1.
相加得an-a1=2(3n-1+3n-2+…+32+3)+n-1,
所以an-a1=2×
| 3(1-3n-1) |
| 1-3 |
所以an=3n+n.
当n=1时,a1=3+1=4成立,
所以an=3n+n.
所以bn=
| n |
| an-n |
| n |
| 3n |
所以Sn=
| 1 |
| 3 |
| 2 |
| 32 |
| 3 |
| 33 |
| n |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 2 |
| 33 |
| 3 |
| 34 |
| n |
| 3n+1 |
①-②,得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| n |
| 3n+1 |
=
| ||||
1-
|
| n |
| 3n+1 |
=
1-
| ||
| 2 |
| n |
| 3n+1 |
∴Sn=
| 3 |
| 4 |
| 1 |
| 4•3n-1 |
| n |
| 2•3n |
(Ⅱ)证明:因为an=3n+n,所以cn=
| n2 |
| (3n+n)-n |
| n2 |
| 3n |
因为cn+1-cn=
| (n+1)2 |
| 3n+1 |
| n2 |
| 3n |
| -2n2+2n+1 |
| 3n+1 |
若-2n2+2n+1<0,则n>
1+
| ||
| 2 |
又因为c1=
| 1 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
点评:本题考查数列的前n项和的求法,考查不等式的证明,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
已知集合A={0,1},B={x∈R|0<x<2},则A∩B=( )
| A、{0} | B、{1} |
| C、[0,1] | D、(0,1) |
已知函数f(x)=2mx3-3nx2+10(m>0)有且仅有两个不同的零点,则lg2m+lg2n的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
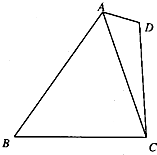 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=
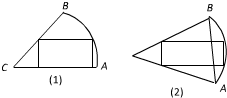 某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.
某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.