题目内容
在△ABC中，A，B，C的对边分别是a，b，c，已知a=1，平面向量
=（sin（π-C），cosC），
=（sin（B+
），sinB），且
•
=sin2A．
（Ⅰ）求△ABC外接圆的面积；
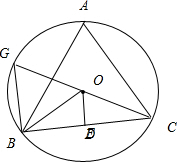
（Ⅱ）已知O为△ABC的外心，由O向边BC、CA、AB引垂线，垂足分别为D、E、F，求
+
+
的值．
| m |
| n |
| π |
| 2 |
| m |
| n |
（Ⅰ）求△ABC外接圆的面积；
（Ⅱ）已知O为△ABC的外心，由O向边BC、CA、AB引垂线，垂足分别为D、E、F，求
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
考点：正弦定理,平面向量数量积的运算
专题：三角函数的求值,解三角形,直线与圆
分析：（Ⅰ）利用向量的数量积，和已知等式化简整理可求得cosA的值，进而求得sinA的值，利用正弦定理求得外接圆的半径，通过圆的面积公式求得答案．
（Ⅱ）分别延长CO交圆于G点，圆内同弦对的∠A和∠G的角相同，进而根据OD∥BG，推断出∠G=∠DOC，进而推断∠BOD=∠A，在RT△BOD中表示出
=cos∠BOE，进而求得
，同理求得
，
，最后相加即可．
（Ⅱ）分别延长CO交圆于G点，圆内同弦对的∠A和∠G的角相同，进而根据OD∥BG，推断出∠G=∠DOC，进而推断∠BOD=∠A，在RT△BOD中表示出
| OD |
| OB |
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
解答：
解：（Ⅰ）∵
•
=sin（π-C）•sin（B+
）+cosC•sinB=sinCcosB+sinBcosC=sin2A．
∴2sinAcosA=sin（B+C）=sinA，
∵0＜A＜π，
∴sinA≠0，
∴2cosA=1，即cosA=
，
∴sinA=
=
∵2R=
=
，
∴R=
，S=πR2=
．
（Ⅱ）∵O为△ABC的外心，由O向边BC、CA、AB引垂线，垂足分别为D、E、F，
延长CO交圆于G点，
∵CG为圆的直径，
∴∠CBG=90°，
OD⊥BC，
∴OD∥BG，
∴∠G=∠DOC，
∵∠A=∠G，∠DOC=∠BOD，
∴∠BOD=∠A，
∵
=cos∠BOE，
∴cosA=
，
∴
=R，
同理可知
=R，
=R，
∴
+
+
=3R=3×
=
．
解：（Ⅰ）∵| m |
| n |
| π |
| 2 |
∴2sinAcosA=sin（B+C）=sinA，
∵0＜A＜π，
∴sinA≠0，
∴2cosA=1，即cosA=
| 1 |
| 2 |
∴sinA=
| 1-cos2A |
| ||
| 2 |
∵2R=
| a |
| sinA |
| 2 | ||
|
∴R=
| ||
| 3 |
| π |
| 3 |
（Ⅱ）∵O为△ABC的外心，由O向边BC、CA、AB引垂线，垂足分别为D、E、F，
延长CO交圆于G点，
∵CG为圆的直径，
∴∠CBG=90°，
OD⊥BC，
∴OD∥BG，
∴∠G=∠DOC，
∵∠A=∠G，∠DOC=∠BOD，
∴∠BOD=∠A，
∵
| OD |
| OB |
∴cosA=
| OD |
| OB |
∴
|
| ||
| cosA |
同理可知
|
| ||
| cosB |
|
| ||
| cosC |
∴
|
| ||
| cosA |
|
| ||
| cosB |
|
| ||
| cosC |
| ||
| 3 |
| 3 |
点评：本题主要考查了正弦定理的应用，三角形外接圆的相关问题．考查了学生基础知识的综合运用．
练习册系列答案
相关题目
设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0]时，f（x）=（
）x-1，若在区间（-2，6）内，函数y=f（x）-loga（x+2），（a＞0，a≠1）恰有1个零点，则实数a的取值范围是（ ）
| ||
| 2 |
| A、（1，4） | ||
| B、（4，+∞） | ||
C、（
| ||
| D、（0，1）∪（1，4） |
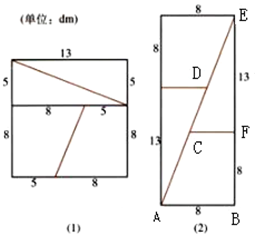魔术大师把一块长和宽都是13dm的地毯按图（1）裁好，再按图（2）拼成矩形．计算两个图形的面积，分别得到169dm2与168dm2．魔术师得意洋洋的说，他证明了169=168．你能揭穿魔术师的奥秘吗？
已知椭圆C1：