Question

1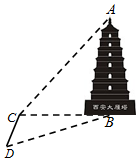．如图，某数学兴趣小组为了测量西安大雁塔高AB，选取与塔底B在同一水平面
内的两个测点C与D．测得∠BCD=105°，∠BDC=45°，CD=26.4m，并在C点测得塔顶A的仰角为60°，则塔高AB=64.68m．（$\sqrt{6}$≈2.45，结果精确到0.01）．

Answer 1

分析 先在△BCD中利用正弦定理计算BC，再在△ABC中求出AB．

解答 解：在△BCD中，∠CBD=180°-45°-105°=30°，
由正弦定理得$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$，即$\frac{BC}{\frac{\sqrt{2}}{2}}=\frac{26.4}{\frac{1}{2}}$，解得BC=26.4×$\sqrt{2}$，
在Rt△ABC中，∵tan∠ACB=$\frac{AB}{BC}$=$\sqrt{3}$，
∴AB=$\sqrt{3}$BC=26.4×$\sqrt{6}$≈64.68．
故答案为：64.68．

点评 本题考查了解三角形的实际应用，属于中档题．