题目内容
18.设复数z=cosθ-sinθ+$\sqrt{2}$+i(cosθ+sinθ),当θ为何值时,|z|取得最大值,并求此最大值.分析 |z|=$\sqrt{(cosθ-sinθ+\sqrt{2})^{2}+(cosθ+sinθ)^{2}}$=$\sqrt{4+4cos(θ+\frac{π}{4})}$.利用三角函数的单调性与值域即可得出.
解答 解:|z|=$\sqrt{(cosθ-sinθ+\sqrt{2})^{2}+(cosθ+sinθ)^{2}}$=$\sqrt{4+2\sqrt{2}(cosθ-sinθ)}$=$\sqrt{4+4cos(θ+\frac{π}{4})}$.
当$cos(θ+\frac{π}{4})$=1时,即θ=2kπ-$\frac{π}{4}$(k∈Z)时,|z|取得最大值为2$\sqrt{2}$.
点评 本题考查了三角函数的单调性与值域、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
10.已知a∈R,i是虚数单位,若z=a+$\sqrt{3}$i,z•$\overline{z}$=4,则a=( )
| A. | 1或-1 | B. | $\sqrt{7}$或-$\sqrt{7}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
11.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
10.在△ABC中,角A、B、C所对的边分别为a,b,c,已知a=1,b=$\sqrt{3}$,A=30°,B为锐角,那么角A:B:C的比值为( )
| A. | 1:1:3 | B. | 1:2:3 | C. | 1:3:2 | D. | 1:4:1 |
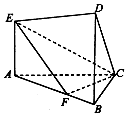 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB