题目内容
10．在△ABC中，角A、B、C所对的边分别为a，b，c，已知a=1，b=$\sqrt{3}$，A=30°，B为锐角，那么角A：B：C的比值为（ ）| A． | 1：1：3 | B． | 1：2：3 | C． | 1：3：2 | D． | 1：4：1 |
分析 由已知及正弦定理可求sinB的值，结合B为锐角，可求B，利用三角形内角和定理可求C，即可得解．
解答 解：∵a=1，b=$\sqrt{3}$，A=30°，B为锐角，
∴由正弦定理可得：sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×sin30°}{1}$=$\frac{\sqrt{3}}{2}$，可得：B=60°，C=180°-A-B=90°，
∴A：B：C=30°：60°：90°=1：2：3．
故选：B．
点评 本题主要考查了正弦定理，三角形内角和定理在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
1．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{5}$，|$\overrightarrow{c}$|=1，若（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）=0，则|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围是（ ）
| A． | [1，2] | B． | [2，4] | C． | [$\sqrt{7}$-1，$\sqrt{7}$+1] | D． | [$\sqrt{5}$-1，$\sqrt{5}$+1] |
5．《数学选修1-2》的知识结构图如图所示，则“直接证明与间接证明”的“上位”要素是（ ）
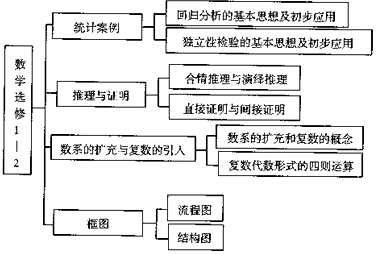
| A． | 推理与证明 | B． | 统计案例 | ||
| C． | 数系的扩充与复数的引入 | D． | 框图 |
2．某公司的组织结构图如图所示，其中技术服务部的直接领导是（ ）
| A． | 董事长 | B． | 监事会 | C． | 总经理 | D． | 总工程师 |
19．已知函数$f（x）=\left\{\begin{array}{l}（{4a-3}）x+2a-4，x≤t\\ 2{x^3}-6x，x＞t\end{array}\right.$，无论t取何值，函数f（x）在R上总是不单调，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | $[{\frac{1}{4}，+∞}）$ | C． | $[{\frac{3}{4}，+∞}）$ | D． | $（{-∞，\frac{3}{4}}]$ |
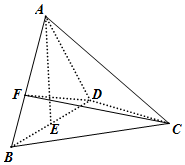如图，在三棱锥A-BCD中，已知△ABD，△BCD都是边长为2的等边三角形，E为BD中点，且AE⊥平面BCD，F为线段AB上一动点，记$\frac{BF}{BA}=λ$．