题目内容
10．已知a∈R，i是虚数单位，若z=a+$\sqrt{3}$i，z•$\overline{z}$=4，则a=（ ）| A． | 1或-1 | B． | $\sqrt{7}$或-$\sqrt{7}$ | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |
分析 求得z的共轭复数，根据复数的运算，即可求得a的值．
解答 解：由z=a+$\sqrt{3}$i，则z的共轭复数$\overline{z}$=a-$\sqrt{3}$i，
由z•$\overline{z}$=（a+$\sqrt{3}$i）（a-$\sqrt{3}$i）=a2+3=4，则a2=1，解得：a=±1，
∴a的值为1或-1，
故选A．
点评 本题考查共轭复数的求法，复数的乘法运算，考查计算能力，属于基础题．
练习册系列答案
相关题目
三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i=1，2，3．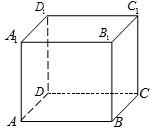
在正方体ABCD-A1B1C1D1中，给出下列结论：
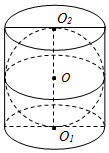如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$．
15．若a＞b＞0，且ab=1，则下列不等式成立的是（ ）
| A． | a+$\frac{1}{b}$＜$\frac{b}{{2}^{a}}$＜log2（a+b）） | B． | $\frac{b}{{2}^{a}}$＜log2（a+b）＜a+$\frac{1}{b}$ | ||
| C． | a+$\frac{1}{b}$＜log2（a+b）＜$\frac{b}{{2}^{a}}$ | D． | log2（a+b））＜a+$\frac{1}{b}$＜$\frac{b}{{2}^{a}}$ |