题目内容
13.已知函数$f(x)=\frac{1}{2}a{x^2}-({2a+1})x+2lnx({x∈R})$(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间.
分析 (Ⅰ)求出原函数的导函数,得到f′(1),f′(3)的值,由f′(1)=f′(3)列式求得a值;
(Ⅱ)f′(x)=$ax-2a-1+\frac{2}{x}$=$\frac{a{x}^{2}-(2a+1)x+2}{x}$(x>0).然后对a分类讨论求得函数的单调区间.
解答 解:(Ⅰ)f′(x)=$ax-2a-1+\frac{2}{x}$,
f′(1)=-a+1,f′(3)=a-$\frac{1}{3}$,
由f′(1)=f′(3),得-a+1=a-$\frac{1}{3}$,
解得a=$\frac{2}{3}$;
(Ⅱ)f′(x)=$ax-2a-1+\frac{2}{x}$=$\frac{a{x}^{2}-(2a+1)x+2}{x}$(x>0).
若a=0,f′(x)=$\frac{-x+2}{x}$.
当x∈(0,2)时,f′(x)>0,当x∈(2,+∞)时,f′(x)<0,
∴函数f(x)的增区间为(0,2),减区间为(2,+∞).
令g(x)=ax2-(2a+1)x+2.
若0<a$<\frac{1}{2}$,方程ax2-(2a+1)x+2=0的两根为x1=2,${x}_{2}=\frac{1}{a}$,且2<$\frac{1}{a}$.
当x∈(0,2)∪($\frac{1}{a}$,+∞)时,g(x)>0,即f′(x)>0;当x∈(2,$\frac{1}{a}$)时,g(x)<0,即f′(x)<0.
∴f(x)的单调增区间为(0,2),($\frac{1}{a}$,+∞);单调减区间为(2,$\frac{1}{a}$).
若a=$\frac{1}{2}$,g(x)≥0,即f′(x)≥0,函数f(x)在(0,+∞)上为增函数.
若a>$\frac{1}{2}$,方程ax2-(2a+1)x+2=0的两根为${x}_{1}=\frac{1}{a}$,x2=2,且$\frac{1}{a}$<2.
当x∈(0,$\frac{1}{a}$)∪(2,+∞)时,g(x)>0,即f′(x)>0;当x∈($\frac{1}{a}$,2)时,g(x)<0,即f′(x)<0.
∴f(x)的单调增区间为(0,$\frac{1}{a}$),(2,+∞);单调减区间为($\frac{1}{a}$,2).
若a<0,程ax2-(2a+1)x+2=0的两根为${x}_{1}=\frac{1}{a}$,x2=2,且$\frac{1}{a}$<0.
当x∈(0,2)时,g(x)>0,即f′(x)>0;当x∈(2,+∞)时,g(x)<0,即f′(x)<0.
∴f(x)的单调增区间为(0,2);单调减区间为(2,+∞).
综上,当a≤0时,f(x)的单调增区间为(0,2);单调减区间为(2,+∞).
当0<a<$\frac{1}{2}$时,f(x)的单调增区间为(0,2),($\frac{1}{a}$,+∞);单调减区间为(2,$\frac{1}{a}$).
当a=$\frac{1}{2}$时,函数f(x)在(0,+∞)上为增函数.
当a$>\frac{1}{2}$时,f(x)的单调增区间为(0,$\frac{1}{a}$),(2,+∞);单调减区间为($\frac{1}{a}$,2).
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查利用导数研究函数的单调性,体现了分类讨论的数学思想方法,是中档题.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案| A. | [1,2] | B. | [2,4] | C. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | D. | [$\sqrt{5}$-1,$\sqrt{5}$+1] |
| A. | 1 | B. | 2 | C. | $\sqrt{3}$+1 | D. | $\sqrt{3}$+2 |
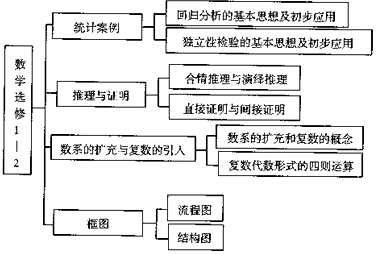
| A. | 推理与证明 | B. | 统计案例 | ||
| C. | 数系的扩充与复数的引入 | D. | 框图 |

| A. | 董事长 | B. | 监事会 | C. | 总经理 | D. | 总工程师 |