题目内容
已知△ABC中,AC=1,∠ABC=
,∠BAC=x,记f(x)=
•
.
(1)求f(x)解析式并标出其定义域;
(2)设g(x)=6mf(x)+1,若g(x)的值域为(1,
],求实数m的值.
| 2π |
| 3 |
| AB |
| BC |
(1)求f(x)解析式并标出其定义域;
(2)设g(x)=6mf(x)+1,若g(x)的值域为(1,
| 3 |
| 2 |
考点:平面向量数量积的运算,正弦定理
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用正弦定理可得BC,AB,再利用数量积运算可得f(x),利用三角形的内角和定理可得其定义域;
(2)对m分类讨论,利用正弦函数的单调性即可得出.
(2)对m分类讨论,利用正弦函数的单调性即可得出.
解答:
解:(1)由正弦定理有:
=
=
;
∴BC=
sinx,AB=
;
∴f(x)=
•
=
sinx•sin(
-x)•
=
(
cosx-
sinx)sinx
=
sin(2x+
)-
,
∵0<x<π-
,∴0<x<
,即函数f(x)的定义域为(0,
).
(2)g(x)=6mf(x)+1=2msin(2x+
)-m+1(0<x<
),
∵x∈(0,
),∴
<2x+
<
,则sin(2x+
)∈(
,1].
当m>0时,g(x)=2msin(2x+
)-m+1的值域为(1,m+1].
又g(x)的值域为(1,
],解得 m=
;
当m<0时,g(x)=2msin(2x+
)-m+1的值域为[m+1,1).
此时m的值不存在.
综上可得:m=
.
| BC |
| sinx |
| 1 | ||
sin
|
| AB | ||
sin(
|
∴BC=
| 1 | ||
sin
|
sin(
| ||
sin
|
∴f(x)=
| AB |
| BC |
| 4 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
=
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| π |
| 6 |
| 1 |
| 6 |
∵0<x<π-
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(2)g(x)=6mf(x)+1=2msin(2x+
| π |
| 6 |
| π |
| 3 |
∵x∈(0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
当m>0时,g(x)=2msin(2x+
| π |
| 6 |
又g(x)的值域为(1,
| 3 |
| 2 |
| 1 |
| 2 |
当m<0时,g(x)=2msin(2x+
| π |
| 6 |
此时m的值不存在.
综上可得:m=
| 1 |
| 2 |
点评:本题考查了正弦定理、数量积运算、三角形的内角和定理、正弦函数的单调性,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
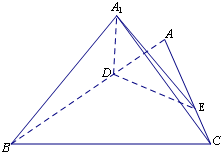 已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足