题目内容
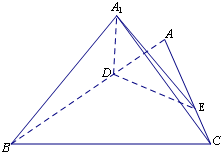 已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(Ⅰ)求证:A1D⊥EC;
(Ⅱ)求三棱锥E-A1CD的高.
考点:平面与平面垂直的性质
专题:综合题,空间位置关系与距离
分析:(Ⅰ)等边△ABC的边长为3,且
=
=
,求得AD和AE的值.进而由余弦定理得DE,根据AD2+DE2=AE2,判断AD⊥DE折叠后A1D⊥DE,根据平面A1DE⊥平面BCED,又平面利用线面垂直的判定定理推断出A1D⊥平面BCED,进而可知A1D⊥EC.
(Ⅱ)求出S△DEC,DC,利用等体积,即可求三棱锥E-A1CD的高.
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(Ⅱ)求出S△DEC,DC,利用等体积,即可求三棱锥E-A1CD的高.
解答:
(Ⅰ)证明:因为等边△ABC的边长为3,且
=
=
,
所以AD=1,AE=2.在△ADE中,∠DAE=60°,
由余弦定理得DE=
.
因为AD2+DE2=AE2,
所以AD⊥DE.
折叠后有A1D⊥DE,
因为平面A1DE⊥平面BCED,又平面A1DE∩平面BCED=DE,
A1D?平面A1DE,A1D⊥DE,所以A1D⊥平面BCED
故A1D⊥EC.…(6分)
(2)因为S△ABC=
,S△ADE=
×1×2sin60°=
,S△DBC=
×3×2sin60°=
所以S△DEC=S△ABC-S△ADE-S△DBC=
-
-
=
…(8分)
又DC2=BD2+BC2-2BD•BCcos60°=4+9-6=7,所以DC=
…(9分)
A1D⊥平面BCED,设三棱锥E-A1CD的高为h,则
•
•A1D=
•
•
•A1D•h,所以h=
所以三棱锥E-A1CD的高为
…(12分)
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
所以AD=1,AE=2.在△ADE中,∠DAE=60°,
由余弦定理得DE=
| 3 |
因为AD2+DE2=AE2,
所以AD⊥DE.
折叠后有A1D⊥DE,
因为平面A1DE⊥平面BCED,又平面A1DE∩平面BCED=DE,
A1D?平面A1DE,A1D⊥DE,所以A1D⊥平面BCED
故A1D⊥EC.…(6分)
(2)因为S△ABC=
9
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
所以S△DEC=S△ABC-S△ADE-S△DBC=
9
| ||
| 4 |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 4 |
又DC2=BD2+BC2-2BD•BCcos60°=4+9-6=7,所以DC=
| 7 |
A1D⊥平面BCED,设三棱锥E-A1CD的高为h,则
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| ||
| 14 |
所以三棱锥E-A1CD的高为
| ||
| 14 |
点评:本题综合考查了线面垂直与平行的判定与性质定理及三棱锥E-A1CD的高,考查了推理能力,属于中档题.

练习册系列答案
相关题目
对于有线性相关关系的变量x,y,测得一组数据如表:
根据表,利用最小二乘法得它们的回归直线方程为
=8.5x+
,据此模型来预测x=20时,y的估计值是( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 60 | 70 |
 |
| y |
 |
| a |
| A、170 | B、175.5 |
| C、177.5 | D、212.5 |
