题目内容
已知Sn是数列{an}的前n项和,且a1=1,nan+1=2Sn(n∈N*),数列{bn}为等比数列,且满足b1=a2,2b3=b4.
(1)求a2的值;
(2)求数列{an},{bn}的通项公式;
(3)求数列{an•bn}的前n项和Tn.
(1)求a2的值;
(2)求数列{an},{bn}的通项公式;
(3)求数列{an•bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由a1=1,nan+1=2Sn(n∈N*),取n=1,能求出a2=2.
(2)当n≥2时,由nan+1=2Sn,得(n-1)an=2Sn-1,故
=
,利用累乘法得an=n(n∈N*).已知b1=a2=2,由2b3=b4,得q=2,从而得到bn=2n.
(3)an•bn=n•2n,由此利用错位相减法能求出数列{an•bn}的前n项和Tn.
(2)当n≥2时,由nan+1=2Sn,得(n-1)an=2Sn-1,故
| an+1 |
| an |
| n+1 |
| n |
(3)an•bn=n•2n,由此利用错位相减法能求出数列{an•bn}的前n项和Tn.
解答:
(本小题满分14分)
解:(1)∵a1=1,nan+1=2Sn(n∈N*),
∴a2=2S1=2a1=2.(2分)
(2)当n≥2时,由nan+1=2Sn,得(n-1)an=2Sn-1(3分)
两式相减,得nan+1-(n-1)an=2(Sn-Sn-1),
即:nan+1=(n+1)an,
∴
=
(4分)
∴a2=2,
=
,
=
,…,
=
,
以上(n-1)个式子相乘得an=2×
×
×…×
×
=n(n≥3),(5分)
又a1=1,a2=2,∴an=n(n∈N*)(6分)
由已知b1=a2=2,设等比数列{bn}的公比为q,
由2b3=b4,得
=2,即q=2(7分)
故bn=2n(8分)
(3)设数列{an•bn}的前n项和Tn,
则Tn=1×2+2×22+3×23+…+n•2n(9分)2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1(11分)
两式相减得-Tn=2+22+23+…+2n-n•2n+1(12分)
=
-n•2n+1(13分)
=-(n-1)•2n+1-2.
故Tn=(n-1)•2n+1+2.(14分)
解:(1)∵a1=1,nan+1=2Sn(n∈N*),
∴a2=2S1=2a1=2.(2分)
(2)当n≥2时,由nan+1=2Sn,得(n-1)an=2Sn-1(3分)
两式相减,得nan+1-(n-1)an=2(Sn-Sn-1),
即:nan+1=(n+1)an,
∴
| an+1 |
| an |
| n+1 |
| n |
∴a2=2,
| a3 |
| a2 |
| 3 |
| 2 |
| a4 |
| a3 |
| 4 |
| 3 |
| an |
| an-1 |
| n |
| n-1 |
以上(n-1)个式子相乘得an=2×
| 3 |
| 2 |
| 4 |
| 3 |
| n-1 |
| n-2 |
| n |
| n-1 |
又a1=1,a2=2,∴an=n(n∈N*)(6分)
由已知b1=a2=2,设等比数列{bn}的公比为q,
由2b3=b4,得
| b4 |
| b3 |
故bn=2n(8分)
(3)设数列{an•bn}的前n项和Tn,
则Tn=1×2+2×22+3×23+…+n•2n(9分)2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1(11分)
两式相减得-Tn=2+22+23+…+2n-n•2n+1(12分)
=
| 2(1-2n) |
| 1-2 |
=-(n-1)•2n+1-2.
故Tn=(n-1)•2n+1+2.(14分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
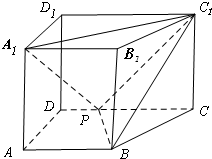 如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=
如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=