题目内容
等差数列{an}，a1=25，a6=15，数列{bn}的前n项和为Sn=2bn-2．（n∈N*）
（1）求数列{an}和{bn}的通项公式；
（2）求数列{
}的前n项和Tn．
（1）求数列{an}和{bn}的通项公式；
（2）求数列{
| an |
| bn |
考点：数列的求和,等差数列的性质
专题：等差数列与等比数列
分析：（1）由等差数列通项公式利用已知条件求出首项和公差，由此能求出an=-2n+27；由Sn=2bn-2，推导出数列{bn}是以2为首项，公比为2的等比数列，从而得到bn=2n．
（2）由
=
，利用错位相减法能求出数列{
}的前n项和Tn．
（2）由
| an |
| bn |
| -2n+27 |
| 2n |
| an |
| bn |
解答：
解：（1）设等差数列{an}的公差为d，则an=a1+（n-1）d，
∴d=
=-2，
∴an=25+（n-1）×（-2）=-2n+27，
∵Sn=2bn-2，∴n=1时，b1=2b1-2，解得b1=2，
当n≥2时，bn=Sn-Sn-1=2bn-2bn-1，
即bn=2bn-1，
∴数列{bn}是以2为首项，公比为2的等比数列，
∴bn=2n．
（2）由（1）知数列
=
，
Tn=
+
+…+
=
+
+…+
，①
Tn=
+
+…+
+
，②
①-②，得：
Tn=
-2(
+
+…+
)-
，
∴
Tn=
-(1-
)-
，
∴Tn=23+
．
∴d=
| a6-a1 |
| 6-1 |
∴an=25+（n-1）×（-2）=-2n+27，
∵Sn=2bn-2，∴n=1时，b1=2b1-2，解得b1=2，
当n≥2时，bn=Sn-Sn-1=2bn-2bn-1，
即bn=2bn-1，
∴数列{bn}是以2为首项，公比为2的等比数列，
∴bn=2n．
（2）由（1）知数列
| an |
| bn |
| -2n+27 |
| 2n |
Tn=
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
=
| 25 |
| 2 |
| 23 |
| 22 |
| -2n+27 |
| 2n |
| 1 |
| 2 |
| 25 |
| 22 |
| 23 |
| 23 |
| -2n+29 |
| 2n |
| -2n+27 |
| 2n+1 |
①-②，得：
| 1 |
| 2 |
| 25 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| -2n+27 |
| 2n+1 |
∴
| 1 |
| 2 |
| 25 |
| 2 |
| 1 |
| 2n-1 |
| -2n+27 |
| 2n+1 |
∴Tn=23+
| 2n-23 |
| 2n |
点评：本题考查数列的通项公式的求法，考查数列的前n项和的求法，解题时要认真审题，注意错位相减法的合理运用．
练习册系列答案
同步奥数系列答案
相关题目
在四面体ABCD中，∠ABC=∠ABD=∠ADC=
，则下列是直角的为（ ）
| π |
| 2 |
| A、∠BCD | B、∠BDC |
| C、∠CBD | D、∠ACD |
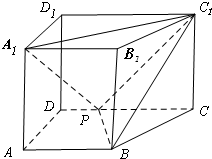如图，直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形，AB∥CD，∠BAD=90°，P是棱CD上一点，AB=2，AD=