题目内容
14．
已知：如图，空间四边形ABCD中，E，F分别是AB，AD的中点．求证：EF∥平面BCD．
分析 连接BD，利用中位线定理证明EF∥BD，即可证明EF∥平面BCD．
解答 
证明：连接BD
因为AE=EB，AF=FD，
所以EF∥BD（三角形中位线的性质）…（5分）
因为EF?平面BCD，BD?平面BCD，
由直线与平面平行的判定定理得EF∥平面BCD…（10分）
点评 本题主要考查了空间中直线与平面平行的证明问题，是基础题目．
练习册系列答案
相关题目
5．已知定义在R上的可导函数f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（-x）=f（2+x），f（2）=1，则不等式f（x）＜ex的解集为（ ）
| A． | （-2，+∞） | B． | （0，+∞） | C． | （1，+∞） | D． | （2，+∞） |
2．
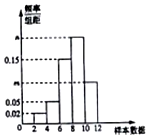有一个容量为100的样本，其频率分布直方图如图所示，已知样本数据落在区间[10，12）内的频数比样本数据落在区间[8，10）内的频数少12，则实数m的值等于（ ）
有一个容量为100的样本，其频率分布直方图如图所示，已知样本数据落在区间[10，12）内的频数比样本数据落在区间[8，10）内的频数少12，则实数m的值等于（ ）| A． | 0.10 | B． | 0.11 | C． | 0.12 | D． | 0.13 |
9．某百货公司1～6月份的销售量x与利润y的统计数据如表：
（1）根据2～5月份的统计数据，求出y关于x的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$）=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$．
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售量x（万件） | 10 | 11 | 13 | 12 | 8 | 6 |
| 利润y（万元） | 22 | 25 | 29 | 26 | 16 | 12 |
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$）=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$．
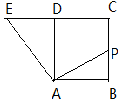如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为BC的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（ ）
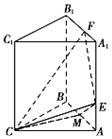在三棱柱ABC-A1B1C1中，CA=CB，侧面ABB1A1是边长为2的正方形，点E，F分别在线段AAl，A1B1上，且AE=$\frac{1}{2}$，A1F=$\frac{3}{4}$，CE⊥EF，M为AB中点