题目内容
9.某百货公司1~6月份的销售量x与利润y的统计数据如表:| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
| 利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$)=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$.
分析 (1)求出$\overline{x}$,$\overline{y}$,由公式,得$\widehat{b}$的值,从而求出$\widehat{a}$的值,从而得到y关于x的线性回归方程,
(2)由(1)能求出该小组所得线性回归方程是理想的.
解答 解:(1)∵$\overline{x}$=11,$\overline{y}$=24,
∴$\widehat{b}$=$\frac{18}{7}$,
故$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=-$\frac{30}{7}$,
故y关于x的方程是:$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$;
(2)∵x=10时,$\widehat{y}$=$\frac{150}{7}$,
误差是|$\frac{150}{7}$-22|=$\frac{4}{7}$<1,
x=6时,$\widehat{y}$=$\frac{78}{7}$,误差是|$\frac{78}{7}$-12|=$\frac{6}{7}$<1,
故该小组所得线性回归方程是理想的.
点评 本题考查了求回归方程问题,考查残差的计算,是一道基础题.

练习册系列答案
相关题目
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )


| A. | f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)在[-$\frac{π}{3}$,0]上单调递增 | |
| C. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| D. | 将函数y=2sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{6}$个单位得到f(x)的图象 |
19.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
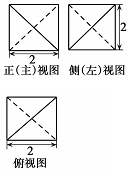

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
 已知:如图,空间四边形ABCD中,E,F分别是AB,AD的中点.
已知:如图,空间四边形ABCD中,E,F分别是AB,AD的中点.