题目内容
已知数列{an}中，an＞0，Sn是数列{an}的前n项和，且an=
，则Sn= ．
| 6Sn |
| an+3 |
考点：数列递推式
专题：等差数列与等比数列
分析：把给出的数列递推式变形，得到6Sn=an2+3an，取n=n+1得另一递推式，作差后得到数列{an}是以3为公差的等差数列，由已知数列递推式求出首项后求得Sn．
解答：
解：由an=
，得6Sn=an2+3an ①，
6Sn+1=an+12+3an+1 ②，
②-①得6an+1=an+12-an2+3an+1-3an，
整理得：（an+1+an）（an+1-an-3）=0．
∵an＞0，
∴an+1+an≠0，
则an+1-an=3．
∴数列{an}是以3为公差的等差数列．
又由an=
，得a1=
，解得：a1=3．
∴Sn=3n+
=
n2+
n．
故答案为：
n2+
n．
| 6Sn |
| an+3 |
6Sn+1=an+12+3an+1 ②，
②-①得6an+1=an+12-an2+3an+1-3an，
整理得：（an+1+an）（an+1-an-3）=0．
∵an＞0，
∴an+1+an≠0，
则an+1-an=3．
∴数列{an}是以3为公差的等差数列．
又由an=
| 6Sn |
| an+3 |
| 6a1 |
| a1+3 |
∴Sn=3n+
| 3n(n-1) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
| 3 |
| 2 |
点评：本题考查了数列递推式，考查了等差关系的确定，考查了等差数列的前n项和公式，是中档题．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
平面α截一个三棱锥，如果截面是梯形，那么平面α必定和这个三棱锥的（ ）
| A、一个侧面平行 |
| B、底面平行 |
| C、仅一条侧棱平行 |
| D、某两条相对的棱都平行 |
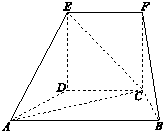如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AB=2BC，∠ABC=60°，且平面CDEF⊥平面ABCD．