Question

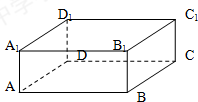长方体ABCD-A₁B₁C₁D₁中，AB=3，BC=2，BB₁=1，由A到C₁在长方体表面上的最短距离为多少

 

．

Answer 1

考点：点、线、面间的距离计算

专题：空间位置关系与距离

分析：求A点到C₁的最短距离，由两点之间直线段最短，想到需要把长方体剪开再展开，把A到C₁的最短距离转化为求三角形的边长问题，根据实际图形，应该有三种展法，展开后利用勾股定理求出每一种情况中AC₁的长度，比较三个值的大小后即可得到结论．

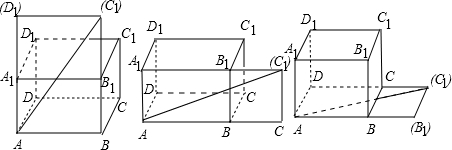
解答： 解：解：长方体ABCD-A₁B₁C₁D₁的表面可有三种不同的方法展开，
如图所示．
，
AB=3，BC=2，BB₁=1．
表面展开后，依第一个图形展开，AC₁=

(1+2)2+32

=3

2

．
依第二个图形展开，AC₁=

(3+2)2+12

=

26

．
依第三个图形展开，AC₁=

(3+1)2+22

=2

5

．
三者比较，得A点沿长方形表面到C₁的最短距离为3

2

．
故答案为：3

2

．

点评：本题考查了点、线、面之间的距离，考查了学生的空间想象能力和思维能力，考查了数学转化思想方法，解答的关键是想到对长方体的三种展法，是中档题．