题目内容
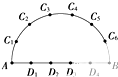 如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( )
如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( )| A、116 | B、128 |
| C、215 | D、98 |
考点:计数原理的应用
专题:排列组合
分析:由题意需要分三类,第一类,3个点全在半圆周上,第二类,二个点在半圆周上,第三类,一个点在半圆周上,根据分类计数原理可得.
解答:
解:由题意需要分三类,第一类,3个点全在半圆周上有
=20个,
第二类,二个点在半圆周上,有
•
=60个,
第三类,一个点在半圆周上,有
=36个,
根据分类计数原理可得,20+60+36=116个.
故选:A.
| C | 3 6 |
第二类,二个点在半圆周上,有
| C | 2 6 |
| C | 1 4 |
第三类,一个点在半圆周上,有
| C | 1 6 |
| •C | 2 4 |
根据分类计数原理可得,20+60+36=116个.
故选:A.
点评:本题主要考查了分类计数原理和分步计数原理,如何分类是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| 1-sin2100° |
| A、cos100° |
| B、±cos100° |
| C、±cos80° |
| D、cos80° |
在极坐标系中,曲线ρ(cosθ+sinθ)=1,则曲线在直角坐标系中方程为( )
| A、x+y=2 | B、x-y=1 |
| C、x=1 | D、x+y=1 |
直线l的方向向量与平面α的法向量的夹角为150°,则l与平面α所成的角为( )
| A、120° | B、30° |
| C、60° | D、150° |
某人朝正东方走xkm后,向左转150°,然后朝新方向走3km,结果它离出发点恰好
km,那么x等于( )
| 3 |
A、
| ||||
B、2
| ||||
C、
| ||||
| D、3 |
已知n是正偶数,用数学归纳法证明某命题时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
| A、n=k+1时命题成立 |
| B、n=k+2时命题成立 |
| C、n=2k+2时命题成立 |
| D、n=2(k+2)时命题成立 |
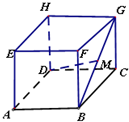 如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )
如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|