题目内容
7.已知$\vec a=(-1,-3,2)$,$\vec b=(1,2,0)$,则$\vec a•\vec b$=( )| A. | -5 | B. | -7 | C. | 3 | D. | $\frac{1}{3}$ |
分析 利用向量空间向量坐标运算法则求解.
解答 解:∵$\vec a=(-1,-3,2)$,$\vec b=(1,2,0)$,
∴$\vec a•\vec b$=-1-6+0=-7.
故选:B.
点评 本题考查空间向量的求法,是基础题,解题时要认真审题,注意向量空间向量坐标运算法则的合理运用.

练习册系列答案
相关题目
15.已知三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且PA=2,PB=$\sqrt{3}$,PC=3,则这个三棱锥的外接球的表面积为( )
| A. | 16π | B. | 32π | C. | 36π | D. | 64π |
2.定义在实数集R上的奇函数分f(x),对任意实数x都有$f(\frac{3}{2}-x)=f(x)$,且满足f(1)>-2,$f(2)=m-\frac{3}{m}$,则实数m的取值范围是( )
| A. | 0<m<3或m<-1 | B. | 0<m<3 | C. | -1<m<3 | D. | m>3或m<-1 |
12.复数$z=\frac{4}{1+i}$(i是虚数单位)的共轭复数在复平面内对应的点是( )
| A. | (2,-2) | B. | (2,2) | C. | (-2,-2) | D. | (-2,2) |
19.设偶函数f(x)的定义域为R,函数g(x)=$\frac{x}{{{x^2}+1}}$,则下列结论中正确的是( )
| A. | |f(x)|g(x)是奇函数 | B. | f(x)g(x)是偶函数 | C. | f(x)|g(x)|是奇函数 | D. | |f(x)g(x)|是奇函数 |
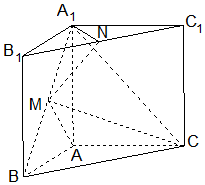 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.