题目内容

17．直线l：4x-y-6=0交双曲线x2-$\frac{{y}^{2}}{4}$=1于A，B两点，则线段AB的长为$\frac{2\sqrt{102}}{3}$．

分析 把y=4x-6代入双曲线方程，利用根与系数关系，求x1+x2和x1x2，再利用弦长公式求线段AB的长．

解答 解：把y=4x-6代入x2-$\frac{{y}^{2}}{4}$=1消去y得3x2-12x+10=0
所以x1+x2=4，x1x2=$\frac{10}{3}$，从而得|AB|=$\sqrt{1+16}•\sqrt{16-4×\frac{10}{3}}$=$\frac{2\sqrt{102}}{3}$，
故答案为$\frac{2\sqrt{102}}{3}$．

点评 本题考查直线与双曲线的位置关系及弦长公式求弦长，比较基础．

练习册系列答案
相关题目
7．已知$\vec a=（-1，-3，2）$，$\vec b=（1，2，0）$，则$\vec a•\vec b$=（　　）
A．-5B．-7C．3D．$\frac{1}{3}$
8．在长方体ABCD-A1B1C1D1中，AA1=AD=4，E是棱CD上的一点．
（1）求证：AD1⊥平面A1B1D；
（2）求证：B1E⊥AD1；
（3）若E是棱CD的中点，在棱AA1上是否存在点P，使得DP∥平面B1AE？若存在，求出线段AP的长；若不存在，请说明理由．
5．在正方体ABCD-A1B1C1D1中，E是棱C1D1的中点，则异面直线A1B、EC的夹角的余弦值为（　　）
A．$\frac{{3\sqrt{10}}}{10}$B．$\frac{{\sqrt{10}}}{10}$C．$\frac{{\sqrt{10}}}{5}$D．$\frac{{\sqrt{15}}}{5}$
12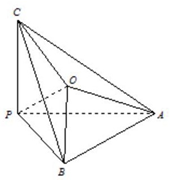．如图，在三棱锥P-ABC中，∠APB=∠BPC=∠APC=90°，O在△ABC内，∠OPC=45°，∠OPA=60°，则∠OPB的余弦值为（　　）
A．$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{6}}{3}$C．$\frac{1}{2}$D．$\frac{\sqrt{2}}{2}$
2．x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$，若z=y-ax取得最大值的最优解不唯一，则实数a的值为（　　）
A．$\frac{1}{2}$或-1B．2或$\frac{1}{2}$C．2或-1D．2或1
9．函数y=x2+bx+c在[0，+∞）上是单调函数的充分条件是（　　）
A．b＞1B．b＜-1C．b＜0D．b＞-1
6．已知定义域为R的函数$f（x）=\frac{{b-{2^x}}}{{a+{2^x}}}$是奇函数．
（1）求a，b的值；
（2）用定义证明f（x）在（-∞，+∞）上为减函数；
（3）若对于任意t∈R，不等式f（t2-2t）＜f（-2t2+k）恒成立，求k的取值范围．
1．若a1、b1、c1、a2、b2、c2∈R，且都不为零，则“$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$”是“关于x的不等式a1x2+b1x+c1＞0与a2x2+b2x+c2＞0的解集相同”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网